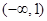题目内容
设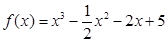 ,当
,当 时,
时,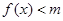 恒成立,则实数
恒成立,则实数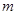 的取值范围为 .
的取值范围为 .
【答案】
(7,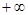 )
)
【解析】
试题分析:根据题意,由于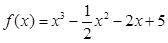 ,且当
,且当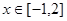 时,
时,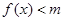 恒成立,则只要m大于函数
恒成立,则只要m大于函数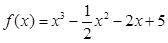 的最大值即可,而
的最大值即可,而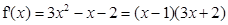 ,
,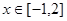 ,可知
,可知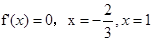 ,因此可知
,因此可知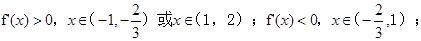 可知函数的 最大值在
可知函数的 最大值在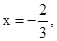 x=2处取得,可知函数的最大值为f(2)=7,故参数m的范围是(7,
x=2处取得,可知函数的最大值为f(2)=7,故参数m的范围是(7,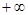 )。
)。
考点:函数的最值
点评:理解不等式的恒成立的求解,就是转化为函数的最值的求解,属于基础题。

练习册系列答案
相关题目
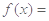
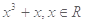 ,当
,当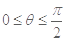 时,
时,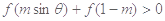 恒成立,则实数
恒成立,则实数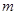 的取值范围是( )
的取值范围是( )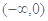 C.
C.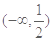 D.
D.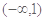
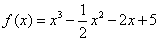 ,当
,当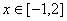 时,
时,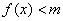 恒成立,则实数
恒成立,则实数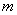 的
的 ,当
,当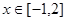 时,
时,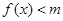 恒成立,则实数
恒成立,则实数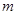 的取值范围为 .[来源:Z.xx.k.Com]
的取值范围为 .[来源:Z.xx.k.Com]

 ,当
,当 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是【 】
的取值范围是【 】 B.
B. C.
C.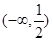 D.
D.