Question

直线y=x+m与曲线x=2

1-y2

只有一个公共点，则m的范围是

-1≤m≤1，或m=-

5

．

Answer 1

分析：由函数的几何意义，作出函数的图象，结合图象得出m的范围．

解答：解：∵x=2

1-y2

，∴

x2

4

+y2=1，
故曲线x=2

1-y2

表示椭圆

x2

4

+y2=1的右半部分，
而直线y=x+m为斜率为1的直线，截距为m，

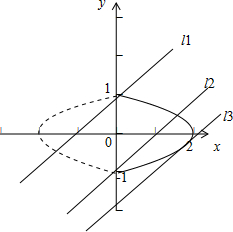
由图可知：当直线介于l₁，l₂之间，或为直线l₃符合题意，
联立

x2 4 +y2=1 y=x+m

，消去y可得5x²+8mx+4m²-4=0，
令△=0，结合图形可得当直线为l₃时，m=-

5

，
故m的范围为：-1≤m≤1，或m=-

5

点评：本题考查函数的零点，由函数的几何意义作出图象是解决问题的关键，属中档题．