题目内容
以下五个命题中,正确命题的个数是 .①不共面的四点中,其中任意三点不共线;
②若a,b,c为空间中不重合的三条直线,若a⊥c,b⊥c,则a∥b;
③对于四面体ABCD,任何三个面的面积之和都大于第四个面的面积;
④对于四面体ABCD,相对棱AB 与CD 所在的直线是异面直线;
⑤各个面都是三角形的几何体是三棱锥.
【答案】分析:对于①可利用反证法进行说明,对于②结合具体实例以及公理定理,进行判断即可,③利用四面体任三个面的面积之和大于第四个面的面积;④⑤依据选项画出几何体的图形,或找出反例即可判断选项的正误.
解答: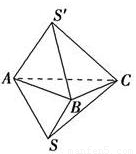 解:①正确,可以用反证法证明,假设任意三点共线,则四个点必共面,与不共面的四点矛盾;
解:①正确,可以用反证法证明,假设任意三点共线,则四个点必共面,与不共面的四点矛盾;
②当a⊥c,b⊥c时,a与b可以相交、平行,也可以异面,故②不正确;
③四面体任三个面的面积之和大于第四个面的面积,故③正确;
④假设相对棱AB与CD所在直线不是异面直线,则有A、B、C、D四点共面,这与四面体ABCD矛盾,故假设不对,故④正确.
⑤如图所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥.∴⑤不正确.
故答案为:3.
点评:本题主要考查了命题的真假判断与应用,考查平面的基本性质及直线与平面的位置关系,是高考中常见的题型,往往学生忽视书本上的基本概念,值得大家注意.
解答:
 解:①正确,可以用反证法证明,假设任意三点共线,则四个点必共面,与不共面的四点矛盾;
解:①正确,可以用反证法证明,假设任意三点共线,则四个点必共面,与不共面的四点矛盾;②当a⊥c,b⊥c时,a与b可以相交、平行,也可以异面,故②不正确;
③四面体任三个面的面积之和大于第四个面的面积,故③正确;
④假设相对棱AB与CD所在直线不是异面直线,则有A、B、C、D四点共面,这与四面体ABCD矛盾,故假设不对,故④正确.
⑤如图所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥.∴⑤不正确.
故答案为:3.
点评:本题主要考查了命题的真假判断与应用,考查平面的基本性质及直线与平面的位置关系,是高考中常见的题型,往往学生忽视书本上的基本概念,值得大家注意.

练习册系列答案
相关题目
 ∥
∥ ;
; 的对称点B的坐标为(3,0);
的对称点B的坐标为(3,0); 的两个焦点坐标为
的两个焦点坐标为 ;
;  ;
; 中,异面直线
中,异面直线 与
与 成
成 的角;
的角; 是水平放置的一个平面图形的直观图,则原图形是一个矩形;
是水平放置的一个平面图形的直观图,则原图形是一个矩形;
