题目内容
已知:a>0 , b>0 , a+b=1,求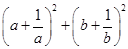 的最小值。
的最小值。
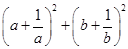 的最小值。
的最小值。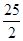
【错解分析】
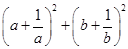 =a2+b2+
=a2+b2+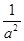 +
+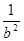 +4
+4≥2ab+
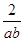 +4
+4≥4
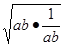 +4=8,
+4=8,∴(a+
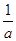 )2+(b+
)2+(b+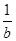 )2的最小值是8.
)2的最小值是8.上面的解答中,两次用到了基本不等式a2+b2≥2ab,第一次等号成立的条件是a=b=
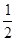 ,第二次等号成立的条件是ab=
,第二次等号成立的条件是ab=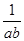 ,显然,这两个条件是不能同时成立的。因此,8不是最小值。
,显然,这两个条件是不能同时成立的。因此,8不是最小值。【正解】原式= a2+b2+
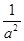 +
+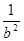 +4
+4="(" a2+b2)+(
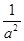 +
+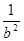 )+4
)+4=[(a+b)2-2ab]+[(
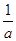 +
+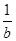 )2-
)2-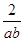 ]+4
]+4= (1-2ab)(1+
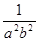 )+4,
)+4,由ab≤(
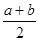 )2=
)2=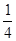 得:1-2ab≥1-
得:1-2ab≥1-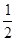 =
=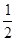 , 且
, 且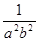 ≥16,1+
≥16,1+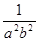 ≥17,
≥17,∴原式≥
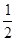 ×17+4=
×17+4=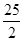 (当且仅当a=b=
(当且仅当a=b=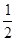 时,等号成立),
时,等号成立),∴(a +
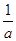 )2 + (b +
)2 + (b + 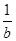 )2的最小值是
)2的最小值是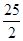 。
。【点评】在应用重要不等式求解最值时,要注意它的三个前提条件缺一不可即“一正、二定、三相等”,在解题中容易忽略验证取提最值时的使等号成立的变量的值是否在其定义域限制范围内。

练习册系列答案
相关题目
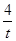 ②.y=sin
②.y=sin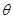 +
+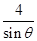 (0<
(0<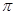 ) ③.y=lgx+4log
) ③.y=lgx+4log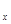 10 ④y=5
10 ④y=5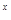 +45
+45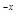
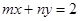 ,
,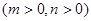 平分圆
平分圆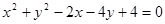 的周长,则
的周长,则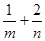 取最小值时,双曲线
取最小值时,双曲线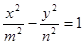 的离心率为 。
的离心率为 。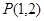 的直线
的直线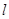 与
与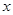 轴正半轴、
轴正半轴、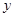 轴正半轴分别交于
轴正半轴分别交于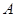 、
、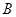 两点,则
两点,则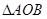 的面积最小为 .
的面积最小为 .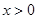 ,不等式
,不等式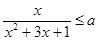 恒成立,则实数
恒成立,则实数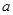 的取值范围是 .
的取值范围是 .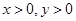 且
且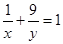 ,求使不等式
,求使不等式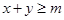 恒成立的实数
恒成立的实数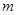 的取值范围是_______
的取值范围是_______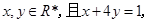 则
则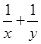 的最小值为
的最小值为 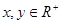 ,且
,且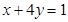 ,则
,则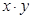 的最大值为 。
的最大值为 。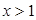 ,则函数
,则函数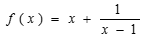 的最小值为
的最小值为