题目内容
在三棱锥O-ABC中,三条棱OA、OB、OC两两相互垂直,且OA>OB>OC,分别过OA、OB、OC作一个截面平分三棱锥的体积,截面面积依次为S1,S2,S3,则S1,S2,S3中的最小值是 .
【答案】分析:取BC中点D,连接OD,AD,则平面OAD平分三棱锥的体积,即三角形OAD面积为S1,由此推导出S12=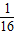 (OA2OB2+OA2OC2).同理可得S22=
(OA2OB2+OA2OC2).同理可得S22=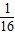 (OA2OB2+OB2OC2),S32=
(OA2OB2+OB2OC2),S32=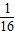 (OA2OC2+OB2OC2),由此能求出S1,S2,S3中的最小值.
(OA2OC2+OB2OC2),由此能求出S1,S2,S3中的最小值.
解答:解:取BC中点D,连接OD,AD,则平面OAD平分三棱锥的体积,
即三角形OAD面积为S1,
在Rt△BOC中,OD是斜边BC上的中线,∴OD= BC,
BC,
∵OA⊥OB,OA⊥OC,∴OA⊥平面BOC,
∵OD?平面BOC,
∴OA⊥OD,
∴S1=OA× OD,
OD,
即S12= OA2OD2=
OA2OD2=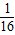 OA2BC2=
OA2BC2=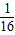 OA2(OB2+OC2)=
OA2(OB2+OC2)=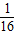 (OA2OB2+OA2OC2).
(OA2OB2+OA2OC2).
同理可得S22=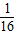 (OA2OB2+OB2OC2),
(OA2OB2+OB2OC2),
S32=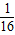 (OA2OC2+OB2OC2),
(OA2OC2+OB2OC2),
因为OA>OB>OC
所以S12>S22>S32
所以S1,S2,S3中的最小值是S3.
故答案为:S3.
点评:本题考查棱锥中截面面积的计算,解题时要认真审题,仔细解答,注意勾股定理的灵活运用.
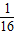 (OA2OB2+OA2OC2).同理可得S22=
(OA2OB2+OA2OC2).同理可得S22=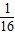 (OA2OB2+OB2OC2),S32=
(OA2OB2+OB2OC2),S32=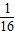 (OA2OC2+OB2OC2),由此能求出S1,S2,S3中的最小值.
(OA2OC2+OB2OC2),由此能求出S1,S2,S3中的最小值.解答:解:取BC中点D,连接OD,AD,则平面OAD平分三棱锥的体积,
即三角形OAD面积为S1,
在Rt△BOC中,OD是斜边BC上的中线,∴OD=
 BC,
BC,∵OA⊥OB,OA⊥OC,∴OA⊥平面BOC,
∵OD?平面BOC,
∴OA⊥OD,
∴S1=OA×
 OD,
OD,即S12=
 OA2OD2=
OA2OD2=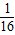 OA2BC2=
OA2BC2=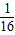 OA2(OB2+OC2)=
OA2(OB2+OC2)=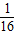 (OA2OB2+OA2OC2).
(OA2OB2+OA2OC2).同理可得S22=
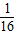 (OA2OB2+OB2OC2),
(OA2OB2+OB2OC2),S32=
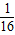 (OA2OC2+OB2OC2),
(OA2OC2+OB2OC2),因为OA>OB>OC
所以S12>S22>S32
所以S1,S2,S3中的最小值是S3.
故答案为:S3.
点评:本题考查棱锥中截面面积的计算,解题时要认真审题,仔细解答,注意勾股定理的灵活运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
