题目内容
已知函数 ,当x=1时有最大值1。当
,当x=1时有最大值1。当 时,函数
时,函数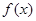 的值域为
的值域为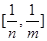 ,则
,则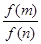 的值为
的值为
 ,当x=1时有最大值1。当
,当x=1时有最大值1。当 时,函数
时,函数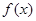 的值域为
的值域为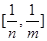 ,则
,则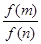 的值为
的值为A. | B. | C. | D. |
D
分析:由x=1时有最大值1,及函数的值域,可知m≥1,从而[m,n]?[1,+∞)因此f(m)=
 ,f(n)=
,f(n)=  ,故可得证.
,故可得证.解:∵函数f(x)=ax2+bx+c,,当x=1时有最大值1,
∴a<0,
∵当x∈[m,n](0<m<n)时,函数f(x)的值域为[
 ,
,  ],
],∴
 ≤1,即m≥1,
≤1,即m≥1,∴[m,n]?[1,+∞),
∴f(m)=
 ,f(n)=
,f(n)=  ,
,∴
 =
= .
.故选D.

练习册系列答案
相关题目
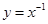 及直线
及直线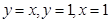 将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数
将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数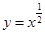 的图象经过的“卦限”是( )
的图象经过的“卦限”是( )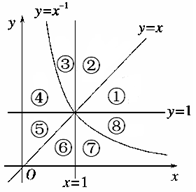
 .
.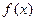 在
在 上是增函数, 求实数a的取值范围.
上是增函数, 求实数a的取值范围.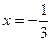 是
是 上的最大值;
上的最大值;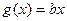 的图像与函数
的图像与函数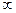 )
) 则
则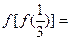 .
. 的图像恒过定点A,若点A在直线
的图像恒过定点A,若点A在直线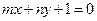 ,
, 上,则
上,则 的最小值是 ▲ .
的最小值是 ▲ . 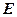 为中心的
为中心的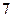 海里以内的海域被设为警戒水域,点
海里以内的海域被设为警戒水域,点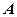 ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点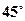 且与点
且与点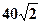 海里的位置
海里的位置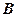 ,经过40分钟又测得该船已经驶到点
,经过40分钟又测得该船已经驶到点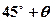 (其中
(其中 且与点
且与点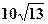 海里的
海里的 处.
处. 求该船的行驶速度;
求该船的行驶速度;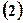 若该船不改变航行
若该船不改变航行 方向继续行驶,判断它是否会进入警戒线水域,并说明理由.
方向继续行驶,判断它是否会进入警戒线水域,并说明理由. +
+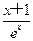 -1.
-1. <
<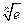 <1+
<1+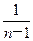 成立.
成立.