题目内容
设平面向量a=(x,y),b=(x2,y2),c=(1,-1),d=(A.0 B.1 C.2 D.4
答案:A
【解析】由已知条件可得a·c=x-y=1;b·d![]() =1.∴
=1.∴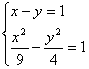 ,由直线x-y=1与双曲线
,由直线x-y=1与双曲线![]() =1无交点可得此方程组无解,即得向量a的个数为0.故应选A.
=1无交点可得此方程组无解,即得向量a的个数为0.故应选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
设平面向量a=(x,y),b=(x2,y2),c=(1,-1),d=(A.0 B.1 C.2 D.4
答案:A
【解析】由已知条件可得a·c=x-y=1;b·d![]() =1.∴
=1.∴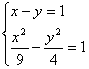 ,由直线x-y=1与双曲线
,由直线x-y=1与双曲线![]() =1无交点可得此方程组无解,即得向量a的个数为0.故应选A.
=1无交点可得此方程组无解,即得向量a的个数为0.故应选A.

 阅读快车系列答案
阅读快车系列答案