题目内容
(本题满分14分)
在平行四边形 中,
中,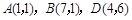 ,点
,点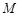 是线段
是线段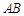 的中点,线段
的中点,线段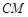 与
与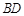 交于点
交于点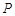 ,
,
(1)求直线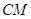 的方程
的方程
(2)求点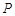 的坐标.
的坐标.
在平行四边形
 中,
中,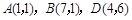 ,点
,点 是线段
是线段 的中点,线段
的中点,线段 与
与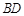 交于点
交于点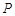 ,
,(1)求直线
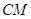 的方程
的方程(2)求点
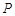 的坐标.
的坐标.
(1)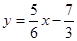 (2)
(2)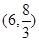
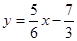 (2)
(2)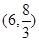
向量是数形结合的典型例子,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,三角函数问题,好多问题都是以向量为载体的.
(1)根据平行四边形 中,
中,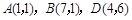 ,点
,点 是线段
是线段 的中点,得到直线CM的方程。
的中点,得到直线CM的方程。
(2)在平行四边形ABCD中,点M是线段AB的中点,得到两个三角形相似,对应边成比例,得到向量之间的关系,设出要求点的坐标,根据向量之间的关系得到向量坐标之间的关系,求出坐标
(1)根据平行四边形
 中,
中,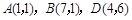 ,点
,点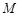 是线段
是线段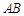 的中点,得到直线CM的方程。
的中点,得到直线CM的方程。(2)在平行四边形ABCD中,点M是线段AB的中点,得到两个三角形相似,对应边成比例,得到向量之间的关系,设出要求点的坐标,根据向量之间的关系得到向量坐标之间的关系,求出坐标

练习册系列答案
相关题目
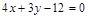 的距离为 .
的距离为 . 、
、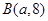 两点的直线与直线
两点的直线与直线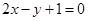 平行,则
平行,则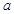
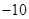
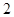
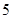
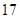
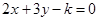 和
和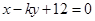 的交点在
的交点在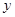 轴上,那么
轴上,那么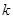 的值是 ( )
的值是 ( )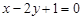 关于直线
关于直线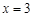 对称的直线方程为 .
对称的直线方程为 . 的图像相切于点
的图像相切于点 ,且
,且 ,
, 为坐标原点,
为坐标原点, 为图像的极大值点,与
为图像的极大值点,与 轴交于点
轴交于点 ,过切点
,过切点 ,则
,则 =
=


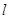 :
: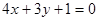 ,则与直线
,则与直线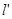 的方程为_________________.
的方程为_________________.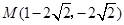 射到
射到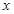 轴上,再反射到圆
轴上,再反射到圆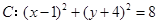 上,求反射点在
上,求反射点在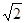 ,0)
,0)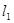 :
: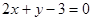 ,
,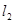 :
: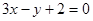 和
和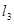 :
: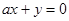 不能构成三角形,则
不能构成三角形,则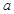 的值为
的值为