题目内容
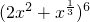的展开式中有理项的个数是
- A.1
- B.2
- C.3
- D.4
C
分析：利用二项展开式的通项公式求出展开式的通项，要使项为有理项，令x的指数为整数，求出r的值，判断出展开式中有理项的个数．
解答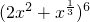：展开式的通项为
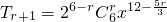
有理项需要x的指数为整数
∴r是3的倍数
∴r=0，3，6
故展开式中有理项的个数是3
故选C
点评：解决二项展开式的特定项问题，应该利用的工具是二项展开式的通项公式．
分析：利用二项展开式的通项公式求出展开式的通项，要使项为有理项，令x的指数为整数，求出r的值，判断出展开式中有理项的个数．
解答：
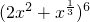展开式的通项为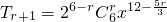有理项需要x的指数为整数
∴r是3的倍数
∴r=0，3，6
故展开式中有理项的个数是3
故选C
点评：解决二项展开式的特定项问题，应该利用的工具是二项展开式的通项公式．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若(x-
)n，n∈N*的展开式中存在至少两个有理项，则n的最小值是（ ）
| 2 | |||
|
| A、2 | B、3 | C、A | D、S |
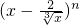，n∈N*的展开式中存在至少两个有理项，则n的最小值是
，n∈N*的展开式中存在至少两个有理项，则n的最小值是（ ）
，n∈N*的展开式中存在至少两个有理项，则n的最小值是（ ）