题目内容
已知α，β为复数，给出下列四个命题：
①若α2∈R，则α∈R或α是纯虚数； ②若|α|=|β|，则α=±β或α=βi；
③若α+β∈R，则α•β∈R或α=
； ④若α+β＞0，且α•β＞0，则α＞0且β＞0
上述命题中假命题的个数是（ ）
①若α2∈R，则α∈R或α是纯虚数； ②若|α|=|β|，则α=±β或α=βi；
③若α+β∈R，则α•β∈R或α=
. |
| β |
上述命题中假命题的个数是（ ）
分析：根据复数乘法的运算法则，我们可由α2∈R，判断出α=a+bi中a=0或b=0，进而判断出①的真假；根据复数的模的定义，根据|α|=|β|，我们可以判断②的真假；根据复数加法的运算法则，及共轭复数的定义，我们可以判断③的真假；根据复数加法和乘法的运算法则，我们可以判断出④的真假，进而得到答案．
解答：解：∵α，β为复数，给出下列四个命题：
①设α=a+bi，则α2=a2-b2+2abi，若α2∈R，则a=0或b=0，故α∈R或α是纯虚数，故①正确；
②设α=a+bi，β=c+di，若|α|=|β|，则a2+b2=c2+d2，即α=±β或α=βi不一定成立，故②错误；
③设α=a+bi，β=c+di，若α+β∈R，则b+d=0，则α•β∈R或α=
不一定成立，故③错误；
④设α=a+bi，β=a-bi，且a＞0，则α+β＞0，且α•β＞0，此时α＞0且β＞0不一定成立，故④错误；
故错误的命题有3个
故选B
①设α=a+bi，则α2=a2-b2+2abi，若α2∈R，则a=0或b=0，故α∈R或α是纯虚数，故①正确；
②设α=a+bi，β=c+di，若|α|=|β|，则a2+b2=c2+d2，即α=±β或α=βi不一定成立，故②错误；
③设α=a+bi，β=c+di，若α+β∈R，则b+d=0，则α•β∈R或α=
. |
| β |
④设α=a+bi，β=a-bi，且a＞0，则α+β＞0，且α•β＞0，此时α＞0且β＞0不一定成立，故④错误；
故错误的命题有3个
故选B
点评：本题考查的知识点是复数的基本概念，复合命题的真假，其中根据复数的基本概念，复数加法、乘法的运算法则，分别判断四个命题的真假，是解答本题的关键．
练习册系列答案
相关题目
，则α∈R或α是纯虚数；
，则α＝±β或α＝βi；
；
，则α＝±β或α＝βi；
；
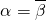； ④若α+β＞0，且α•β＞0，则α＞0且β＞0