题目内容
设动直线x=a与函数f(x)=2sin2(| π |
| 4 |
| 3 |
分析:本题考查的是正弦型函数的性质,由设动直线x=a与函数f(x)=2sin2(
+x)和g(x)=
cos2x的图象分别交于M、N两点,则:|MN|=|f(x)-g(x)|,将两个函数的解析式代入化简为正弦型函数,再由正弦型函数的性质即可得到结论.
| π |
| 4 |
| 3 |
解答:解:|MN|=|f(x)-g(x)|
=|2sin2(
+x)-
cos2x|
=|1-cos(2x+
)-
cos2x|
=|sin2x-
cos2x+1|
=|2sin(2x-
)+1|
∴|MN|的最大值为3
故答案为3
=|2sin2(
| π |
| 4 |
| 3 |
=|1-cos(2x+
| π |
| 2 |
| 3 |
=|sin2x-
| 3 |
=|2sin(2x-
| π |
| 3 |
∴|MN|的最大值为3
故答案为3
点评:函数y=Asin(ωx+φ)(A>0,ω>0)中,最大值或最小值由A确定,由周期由ω决定,即要求三角函数的周期与最值一般是要将其函数的解析式化为正弦型函数,再根据最大值为|A|,最小值为-|A|,周期T=
进行求解.
| 2π |
| ω |

练习册系列答案
相关题目
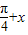 )和g(x)=
)和g(x)=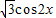 的图象分别交于M、N两点,则|MN|的最大值为 .
的图象分别交于M、N两点,则|MN|的最大值为 .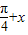 )和g(x)=
)和g(x)=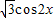 的图象分别交于M、N两点,则|MN|的最大值为 .
的图象分别交于M、N两点,则|MN|的最大值为 .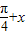 )和g(x)=
)和g(x)=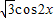 的图象分别交于M、N两点,则|MN|的最大值为 .
的图象分别交于M、N两点,则|MN|的最大值为 .