题目内容
如图,☉O和☉O′相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连结DB并延长交☉O于点E.证明:
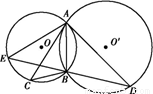
(1)AC·BD=AD·AB;
(2)AC=AE.
【答案】
见解析
【解析】
证明:(1)由AC与☉O′相切于A,得∠CAB=∠ADB,
同理∠ACB=∠DAB,
所以△ACB∽△DAB,从而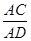 =
=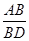 ,
,
即AC·BD=AD·AB.
(2)由AD与☉O相切于A,得∠AED=∠BAD,
又∠ADE=∠BDA,得△EAD∽△ABD.
从而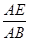 =
=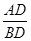 ,
,
即AE·BD=AD·AB,
结合(1)的结论,AC=AE.

练习册系列答案
相关题目
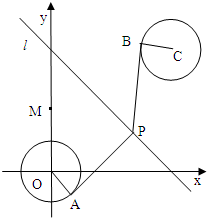 已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
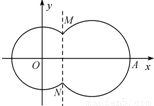
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|; (2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).
(2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).

 是平面PAC内的两条相较直线,所以BD
是平面PAC内的两条相较直线,所以BD 平面PAC,
平面PAC, 平面PAC,所以
平面PAC,所以 .
. 是直线PD和平面PAC所成的角,从而
是直线PD和平面PAC所成的角,从而 .
. 平面PAC,知
平面PAC,知 .在
.在 中,由
中,由 ,所以
,所以 均为等腰直角三角形,从而梯形ABCD的高为
均为等腰直角三角形,从而梯形ABCD的高为 于是梯形ABCD面积
于是梯形ABCD面积 在等腰三角形AOD中,
在等腰三角形AOD中,

 的体积为
的体积为 .
.
 算得体积
算得体积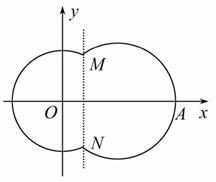
 PO?若存在,指出有几个这样的点;若不存在,请说明理由;
PO?若存在,指出有几个这样的点;若不存在,请说明理由;