题目内容
已知椭圆的右焦点F与抛物线y2=4x的焦点重合,短轴长为2.椭圆的右准线l与x轴交于E,过右焦点F的直线与椭圆相交于A、B两点,点C在右准线l上,BC∥x轴.
(1)求椭圆的标准方程,并指出其离心率;
(2)求证:线段EF被直线AC平分.
解:(1)由题意,可设椭圆的标准方程为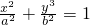 (a>b>0)
(a>b>0)
∵y2=4x的焦点为F(1,0)
∴c=1,又2b=2,
∴b=1,a2=b2+c2=2,
所以,椭圆的标准方程为
其离心率为e=
(2)证明:∵椭圆的右准线1的方程为:x=2,
∴点E的坐标为(2,0)设EF的中点为M,则M( ,0)
,0)
若AB垂直于x轴,则A(1,y1),B(1,-y1),C(2,-y1)
∴AC的中点为N( ,0)
,0)
∴线段EF的中点与AC的中点重合,
∴线段EF被直线AC平分,
若AB不垂直于x轴,则可设直线AB的方程为
y=k(x-1),k≠0,A(x1,y1),B(x2,y2)
则C(2,-y2)
把y=k(x-1)代入
得(1+2k2)x2-4k2x+2(k2-1)=0
则有x1+x2=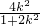 ,x1x2=
,x1x2=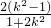
∴kAM=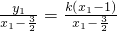
=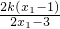 ,kCM=
,kCM=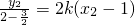 ,
,
∵kAM-kCM=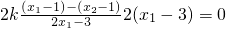
=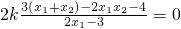
∴kAM=kCM
∴A、M、C三点共线,即AC过EF的中点M,
∴线段EF被直线AC平分.
分析:(1)先设出椭圆的标准方程,根据抛物线的方程求得其焦点坐标,进而求得椭圆的c,短半轴b求得a,则椭圆的方程和离心率可得.
(2)根据(1)中的椭圆方程求得其准线l的方程,求得点E的坐标,设EF的中点为M,则M的坐标可得,先看当AB垂直于x轴,则设出点A,B,C的坐标,求得AC中点的坐标,判断出线段EF的中点与AC的中点重合;再看AB不垂直于x轴,则可设直线AB的方程与椭圆方程联立消去y,根据韦达定理表示出x1+x2和x1x2的表达式,可表示出AM和CM的斜率,求得二者相等,进而推断出A、M、C三点共线,即AC过EF的中点M,最后综合证明题设.
点评:本题主要考查了圆锥曲线的综合运用.考查了学生综合分析问题和分类讨论思想的运用.属中档题.
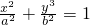 (a>b>0)
(a>b>0)∵y2=4x的焦点为F(1,0)
∴c=1,又2b=2,
∴b=1,a2=b2+c2=2,
所以,椭圆的标准方程为

其离心率为e=

(2)证明:∵椭圆的右准线1的方程为:x=2,
∴点E的坐标为(2,0)设EF的中点为M,则M(
 ,0)
,0)若AB垂直于x轴,则A(1,y1),B(1,-y1),C(2,-y1)
∴AC的中点为N(
 ,0)
,0)∴线段EF的中点与AC的中点重合,
∴线段EF被直线AC平分,
若AB不垂直于x轴,则可设直线AB的方程为
y=k(x-1),k≠0,A(x1,y1),B(x2,y2)
则C(2,-y2)
把y=k(x-1)代入

得(1+2k2)x2-4k2x+2(k2-1)=0
则有x1+x2=
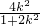 ,x1x2=
,x1x2=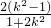
∴kAM=
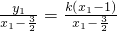
=
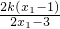 ,kCM=
,kCM=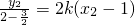 ,
,∵kAM-kCM=
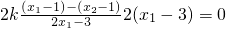
=
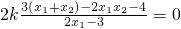
∴kAM=kCM
∴A、M、C三点共线,即AC过EF的中点M,
∴线段EF被直线AC平分.
分析:(1)先设出椭圆的标准方程,根据抛物线的方程求得其焦点坐标,进而求得椭圆的c,短半轴b求得a,则椭圆的方程和离心率可得.
(2)根据(1)中的椭圆方程求得其准线l的方程,求得点E的坐标,设EF的中点为M,则M的坐标可得,先看当AB垂直于x轴,则设出点A,B,C的坐标,求得AC中点的坐标,判断出线段EF的中点与AC的中点重合;再看AB不垂直于x轴,则可设直线AB的方程与椭圆方程联立消去y,根据韦达定理表示出x1+x2和x1x2的表达式,可表示出AM和CM的斜率,求得二者相等,进而推断出A、M、C三点共线,即AC过EF的中点M,最后综合证明题设.
点评:本题主要考查了圆锥曲线的综合运用.考查了学生综合分析问题和分类讨论思想的运用.属中档题.

练习册系列答案
相关题目