题目内容
有下列命题:①过双曲线xy=k(k>0)上任意一点的切线与两坐标轴围成的三角形的面积为
| 2 |
②曲线xy=k(k>0)关于原点对称;
③一系列双曲线xy=(
| 1 |
| 4 |
| 2 |
④“xy=k(k>0)被直线x+y=2
| 2k |
| 2k |
分析:通过判断函数的奇偶性得到函数的对称轴;通过双曲线的实轴长公式求出实轴长的和.
解答:解:xy=k即y=
,
令f(x)=
,
∵f(-x)=
=-
=-f(x),
∴f(x)为奇函数故其图象关于原点对称故②正确;
一系列双曲线xy=(
)n(n=1,2,3,…),
所有这些双曲线的实轴长之和为2
故答案为②③.
| k |
| x |
令f(x)=
| k |
| x |
∵f(-x)=
| k |
| -x |
| k |
| x |
∴f(x)为奇函数故其图象关于原点对称故②正确;
一系列双曲线xy=(
| 1 |
| 4 |
所有这些双曲线的实轴长之和为2
| 2 |
故答案为②③.
点评:本题考查判断函数的奇偶性判断出函数的对称性、双曲线的弦长公式、实轴长的公式.

练习册系列答案
相关题目
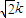 ;
; ,所有这些双曲线的实轴长之和为
,所有这些双曲线的实轴长之和为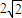 ;
;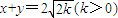 所截得的线段与x2-y2=k(k>0)被直线
所截得的线段与x2-y2=k(k>0)被直线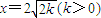 所截得的线段相等”是必然事件.其中所有真命题的序号是 .
所截得的线段相等”是必然事件.其中所有真命题的序号是 .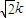 ;
;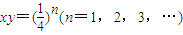 ,所有这些双曲线的实轴长之和为
,所有这些双曲线的实轴长之和为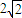 ;
;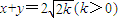 所截得的线段与x2-y2=k(k>0)被直线
所截得的线段与x2-y2=k(k>0)被直线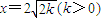 所截得的线段相等”是必然事件.其中所有真命题的序号是 .
所截得的线段相等”是必然事件.其中所有真命题的序号是 .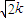 ;
;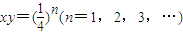 ,所有这些双曲线的实轴长之和为
,所有这些双曲线的实轴长之和为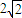 ;
; 所截得的线段与x2-y2=k(k>0)被直线
所截得的线段与x2-y2=k(k>0)被直线 所截得的线段相等”是必然事件.其中所有真命题的序号是 .
所截得的线段相等”是必然事件.其中所有真命题的序号是 .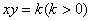 上任意一点的
上任意一点的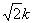 ;
; 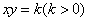 关于原点对称;③一系列双曲线
关于原点对称;③一系列双曲线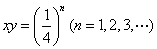 ,所有这些双曲线的实轴长之和为
,所有这些双曲线的实轴长之和为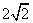 ;④“
;④“ 所截得的线段与
所截得的线段与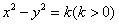 被直线
被直线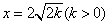 所截得的线段相等”是必然事件.
所截得的线段相等”是必然事件.