��Ŀ����
ij�̳���100Ԫ/���ļ۸�һ�����£��Ը��ڽ��۵ļ۸���ۣ������е���������֮�֣�ͨ���г����鷢�֣���������r(x)(��)����±��x(Ԫ/��)�������������Ƶط��Ϻ�����ϵr(x)=kx+b1�������۵������Ƶط��Ϻ�����ϵr(x)=kx+b2������k��0��b1��0��b2��0,��k,b1,b2Ϊ����.
���������������̳���140Ԫ/���ļ۸������ܻ�������������
�����Ƣ���r(x)=0ʱ�ı��xΪ���µġ��ٽ�۸������������ġ��ٽ�۸������۵����ġ��ٽ�۸�1.5��.
�����������Ϣ������������⣺
(1)��������пո�����ݣ�
������ϵ ���ۼ��� | ���(Ԫ/��) | ������r(x)(��) (��k��b1��b2) | ��ͬ���ڵ�����������y(Ԫ)����x(Ԫ/��)�ĺ�����ϵʽ |
���� | x | r(x)=kx+b1 |
|
���� | x |
|
|
(2)�����۵��������̳�Ҫ���������������±��Ӧ��Ϊ����Ԫ�ź��ʣ�
˼·������(1)������������y=������r(x)��ÿ������ÿ������=���-���ۣ�(2)ת��Ϊ����κ���y=f(x)�����ֵ���������ڢ����b2��k�Ĺ�ϵ��Ӧ�ö��κ�����֪ʶ���.
�⣺(1)������������y=(kx+b1)(x-100)=kx2-(100k-b1)x-100b1��
�����۵�����y=(kx+b2)(x-100)=kx2-(100k-b2)x-100b2��
�����������±���ʾ:
������ϵ ���ۼ��� | ���(Ԫ/��) | ������r(x)(��) (��k��b1��b2) | ��ͬ���ڵ�����������y(Ԫ)����x(Ԫ/��)�ĺ�����ϵʽ |
���� | x | r(x)=kx+b1 | y=kx2-(100k-b1)x-100b1 |
���� | x | r(x)=kx+b2 | y=kx2-(100k-b2)x-100b2 |
(2)��k��0��b1��0��b2��0.��![]() ��0��
��0��![]() ��0.
��0.
��50-![]() ��0��50
��0��50![]() ��0.
��0.
��������������y=kx2-(100k-b1)x-100b1��
�൱x=![]() =50
=50![]() ʱ������yȡ���ֵ��
ʱ������yȡ���ֵ��
�����۵�����y=kx2-(100k-b2)x-100b2��
�൱x=![]() =50
=50![]() ʱ������yȡ���ֵ.
ʱ������yȡ���ֵ.
�ɢ�֪���������������̳���140Ԫ/���ļ۸����ʱ���ܻ���������
��������������������x=50![]() =140ʱ������yȡ���ֵ.��b1=-180k.
=140ʱ������yȡ���ֵ.��b1=-180k.
���ʱ������Ϊr(x)=kx-180k.��kx-180k=0����x=180��
�����������������µġ��ٽ�۸�Ϊ180Ԫ/��.
���ɢ�֪�������۵��������µġ��ٽ�۸�Ϊ180��![]() =120Ԫ/��.
=120Ԫ/��.
�ɼ������۵����������x=120Ԫ/��ʱ��������Ϊr(x)=kx+b2=0.
��120k+b2=0.��![]() =-120.
=-120.
�������۵����������x=50![]() =50��60=110Ԫ/��ʱ������yȡ�����ֵ,
=50��60=110Ԫ/��ʱ������yȡ�����ֵ,
�������۵������̳�Ҫ����������Ӧ�����µı�۶�Ϊ110Ԫ/���ź���.

����С������12�֣�ij�̳���100Ԫ/���ļ۸�һ�����£��Ը��ڽ��۵ļ۸���ۣ������е�������֮��.ͨ���г����鷢�֣���������![]() ����������±��x��Ԫ/�����������������Ƶط��Ϻ�����ϵ��
����������±��x��Ԫ/�����������������Ƶط��Ϻ�����ϵ��![]() �������۵������Ƶط��Ϻ�����ϵ��
�������۵������Ƶط��Ϻ�����ϵ��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ���������������������̳���140Ԫ/���ļ۸������ܻ����������������Ƣ���
Ϊ���������������������̳���140Ԫ/���ļ۸������ܻ����������������Ƣ���![]() ʱ�ı��xΪ���µġ��ٽ�۸������������ġ��ٽ�۸������۵����ġ��ٽ�۸�1.5��.
ʱ�ı��xΪ���µġ��ٽ�۸������������ġ��ٽ�۸������۵����ġ��ٽ�۸�1.5��.
�����������Ϣ������������⣺
������������пո�����ݣ�
| ������ϵ ���ۼ��� | ��� ��Ԫ/���� | ������ ����k��b1��b2�� | ��ͬ���ڵ�����������y��Ԫ�� ����x��Ԫ/�����ĺ�����ϵʽ |
| �� �� | x |
| |
| �� �� | x |
���������۵��������̳�Ҫ���������������µı��Ӧ��Ϊ����Ԫ�ź��ʣ�
����С������12�֣�ij�̳���100Ԫ/���ļ۸�һ�����£��Ը��ڽ��۵ļ۸���ۣ������е�������֮��.ͨ���г����鷢�֣���������![]() ����������±��x��Ԫ/�����������������Ƶط��Ϻ�����ϵ��
����������±��x��Ԫ/�����������������Ƶط��Ϻ�����ϵ��![]() �������۵������Ƶط��Ϻ�����ϵ��
�������۵������Ƶط��Ϻ�����ϵ��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ���������������������̳���140Ԫ/���ļ۸������ܻ����������������Ƣ���
Ϊ���������������������̳���140Ԫ/���ļ۸������ܻ����������������Ƣ���![]() ʱ�ı��xΪ���µġ��ٽ�۸������������ġ��ٽ�۸������۵����ġ��ٽ�۸�1.5��.
ʱ�ı��xΪ���µġ��ٽ�۸������������ġ��ٽ�۸������۵����ġ��ٽ�۸�1.5��.
�����������Ϣ������������⣺
������������пո�����ݣ�
| ������ϵ ���ۼ��� | ��� ��Ԫ/���� | ������ ����k��b1��b2�� | ��ͬ���ڵ�����������y��Ԫ�� ����x��Ԫ/�����ĺ�����ϵʽ |
| �� �� | x |
| |
| �� �� | x |
���������۵��������̳�Ҫ���������������µı��Ӧ��Ϊ����Ԫ�ź��ʣ�
(��������14��)
ij�̳���100Ԫ/���ļ۸�һ�����£��Ը��ڽ����۵ļ۸���ۣ��������е���������֮�֣�ͨ���г����鷢�֣�
�������� (��)����±��
(��)����±�� (Ԫ/��)�������������Ƶط��Ϻ�����ϵ��
(Ԫ/��)�������������Ƶط��Ϻ�����ϵ�� �������۵������Ƶط��Ϻ�����ϵ��
�������۵������Ƶط��Ϻ�����ϵ�� ������
������ ������
������
���������������̳���140Ԫ/���ļ۸������ܻ�������������
�����Ƣ��� ʱ�ı��
ʱ�ı�� Ϊ���µġ��ٽ�۸������������ġ��ٽ�۸������۵����ġ��ٽ�۸�1.5����
Ϊ���µġ��ٽ�۸������������ġ��ٽ�۸������۵����ġ��ٽ�۸�1.5����
�����������Ϣ������������⣺
(��)��������пո�����ݣ�
|
���۹�ϵ |
���(Ԫ/��) |
������ |
���������� (Ԫ/��)�ĺ�����ϵʽ |
|
���� |
|
|
|
|
���� |
|
|
|
(��)�����۵��������̳�Ҫ���������������µı��Ӧ��Ϊ����Ԫ/����
 ������ϵ
������ϵ ��
�� ��
�� )
)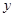 (Ԫ)����
(Ԫ)����