题目内容
已知抛物线C:y=
x2在点A处的切线l与直线l':y=x+1平行.
(1)求A点坐标和直线l的方程;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.
| 1 | 4 |
(1)求A点坐标和直线l的方程;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.
分析:(1)先设切线方程,联立切线方程与抛物线方程,根据A为切点,方程只有一组解求出直线l的方程;进而求出A点坐标;
(2)先根据圆A的半径r等于圆心A到的距离求出半径即可得到结论.
(2)先根据圆A的半径r等于圆心A到的距离求出半径即可得到结论.
解答:解:(1)设抛物线C:y=
x2在点A处的切线l的方程为:y=x+b ①,
由
⇒x2-4x-4b=0.②
令△=42-4×(-4b)=0⇒b=-1,代入②得x=2,结合①得y=1
所以:A(2,1),直线l的方程为y=x-1.
(2)抛物线的准线为y=-1,所以圆A的半径r等于圆心A到的距离,即r=2.
所以圆A的方程为(x-2)2+(y-1)2=4.
| 1 |
| 4 |
由
|
令△=42-4×(-4b)=0⇒b=-1,代入②得x=2,结合①得y=1
所以:A(2,1),直线l的方程为y=x-1.
(2)抛物线的准线为y=-1,所以圆A的半径r等于圆心A到的距离,即r=2.
所以圆A的方程为(x-2)2+(y-1)2=4.
点评:本题主要考察圆与圆锥曲线的综合问题.解决第一问的关键在于设切线方程,联立切线方程与抛物线方程,根据A为切点,方程只有一组解求出直线l的方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
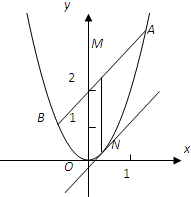 已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.