题目内容
棱长为2的正方体 在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则点
在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则点 到原点O的最远距离为( )
到原点O的最远距离为( )
A. B.
B. C.5 D.4
C.5 D.4
D
解析试题分析:根据题意,由于棱长为2的正方体 在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则可知设A(X,0)b(0,y),可知
在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则可知设A(X,0)b(0,y),可知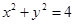 ,那么可以设
,那么可以设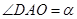 ,那么可知
,那么可知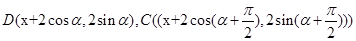 借助于三角函数的性质可知CO的最大值为
借助于三角函数的性质可知CO的最大值为 ,那么可知点
,那么可知点 到原点O的最远距离为4,选D.
到原点O的最远距离为4,选D.
考点:展开图,正方体
点评:求解空间一点到坐标原点的距离的最值问题,转化为求点在平面内的射影到原点的距离的最大值即可,属于中档题,考查分析问题的能力。

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为 ( ) 
A. | B. | C. | D. |
已知某四棱锥的三视图(单位:cm)如图所示,则该四棱锥的体积是
A. | B. | C. | D.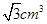 |
如图在棱长为5的正方体 中,
中, 是棱
是棱 上的一条线段,且
上的一条线段,且 ,
, 是
是 中点,点
中点,点 是棱
是棱 上动点,则四面体
上动点,则四面体 的体积( )
的体积( )
| A.是变量且有最大值 | B.是变量且有最小值 |
| C.是变量且有最大值和最小值 | D.是常量 |
一个几何体的三视图如图所示,则该几何体的体积为( )
| A.25 | B.36 | C.12 | D.24 |
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形. 则该几何体的体积为( )
| A.16 | B.48 |
| C.60 | D.96 |
右图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧视图的面积为( )
A. | B.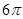 | C. | D. |
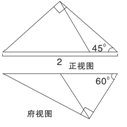
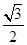
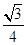
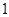
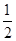
 的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去
的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去 个三棱锥后 ,剩下的几何体的体积是( )
个三棱锥后 ,剩下的几何体的体积是( )


