题目内容
定义f(M)=(m,n,p),其中M是△ABC内一点,m,n,p分别是△MBC,△MCA,△MAB的面积,已知在△ABC中,
•
=2
,∠BAC=30°,f(M)=(
,x,y),则
+
的最小值是
| AB |
| AC |
| 3 |
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
18
18
.分析:先利用条件确定x,y的关系式为2x+2y=1,然后利用基本不等式求最小值.注意1的等价代换.
解答:解:因为在△ABC中,
•
=2
,∠BAC=30°,所以|
|?|
|cos?30?=2
,即|
|?|
|=4.
所以S△ABC=
|
|?|
|sin30?=
×4×
=1,由
f(M)=(
,x,y),得x+y=
.即2x+2y=1.
所以
+
=(
+
)(2x+2y)=10+
+
≥10+2
=10+8=18,
当且仅当
=
,即y2=4x2时取等号,
所以
+
的最小值是18.
故答案为:18.
| AB |
| AC |
| 3 |
| AC |
| AB |
| 3 |
| AC |
| AB |
所以S△ABC=
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
f(M)=(
| 1 |
| 2 |
| 1 |
| 2 |
所以
| 1 |
| x |
| 4 |
| y |
| 1 |
| x |
| 4 |
| y |
| 2y |
| x |
| 8x |
| y |
|
当且仅当
| 2y |
| x |
| 8x |
| y |
所以
| 1 |
| x |
| 4 |
| y |
故答案为:18.
点评:本题考查了基本不等式的应用,先通过新定义建立x,y的关系式是解决本题的关键,在解题过程中,要注意“1”的代换.

练习册系列答案
相关题目
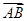 ·
·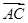 =2
=2 ,∠BAC=30°,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(
,∠BAC=30°,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(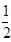 ,x,y),则
,x,y),则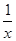 +
+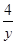 的最小值是 .
的最小值是 . =2
=2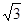 ,∠BAC=30°定义f(M)=(m,n,p),其中m,n,p分别是△MBC,△MCA, △MAB的面积.若f(M)=(
,∠BAC=30°定义f(M)=(m,n,p),其中m,n,p分别是△MBC,△MCA, △MAB的面积.若f(M)=( ,x,y),则
,x,y),则 的最小值是
的最小值是 的最大值和最小值分别为M和N,则M+N= .
的最大值和最小值分别为M和N,则M+N= .