题目内容
(本小题满分14分)
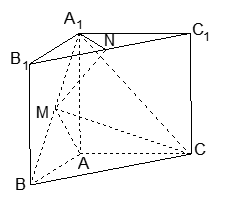
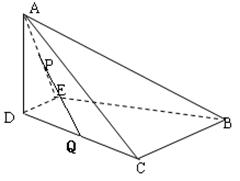
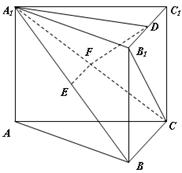
在三棱锥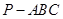 中,
中,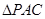 和
和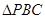 都是边长为
都是边长为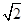 的等边三角形,
的等边三角形,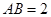 ,
,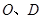 分别是
分别是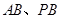 的中点.
的中点.
(1)求证: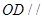 平面
平面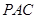 ;
;
(2)求证:平面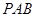 ⊥平面
⊥平面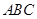 ;
;
(3)求三棱锥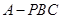 的体积.
的体积.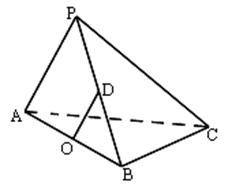
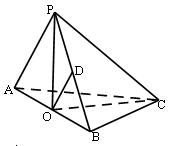
(1)见解析 (2) 见解析;
(3)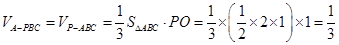 。
。
解析试题分析:(1)根据线面平行的判定定理,只须判定OD//PA即可.
(2)根据面面垂直的判定只须证明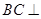 平面PAB即可.
平面PAB即可.
(3)在(1)(2)的基础上,可利用三棱锥可换底的特性知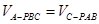 .
.
解:(1) 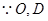 分别为
分别为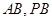 的中点,
的中点, 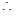
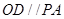 ·······2分
·······2分
又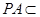 平面
平面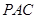 ,
,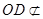 平面
平面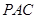
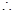
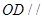 平面
平面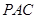 ·······4分
·······4分
(2) 连结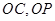
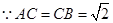 ,
, 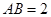 ,
, 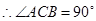
又 为
为 的中点,
的中点,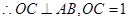 ,
,
同理, 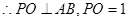 ·······6分
·······6分
又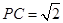 ,
, 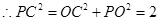 ,
,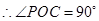
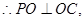 ·······8分
·······8分
又 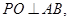
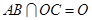 ,
,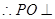 平面
平面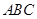 .
.
由于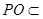 平面
平面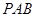 ,
, 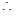 平面
平面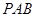 ⊥平面
⊥平面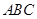 ·······10分
·······10分
(3)由(2)可知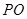 ⊥平面
⊥平面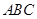
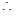
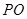 为三棱锥
为三棱锥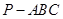 的高,且
的高,且 ·······11分
·······11分
故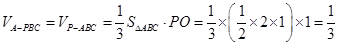 ·······14分
·······14分
考点:线面平行,线面垂直,面面垂直的判定及性质,三棱锥的体积.
点评:掌握线线,线面,面面平行与垂直的判定与性质是解决此类的前提,勿必熟记,同是在求三棱锥体积时,要注意可换底的特性.

练习册系列答案
相关题目

 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
,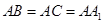
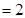 ,点
,点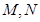 分别为
分别为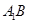 和
和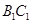 的中点.
的中点.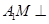 平面
平面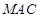 ;
;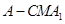 的体积;
的体积;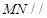 平面
平面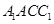 .
.
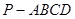 的侧面
的侧面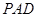 垂直于底面
垂直于底面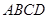 ,
,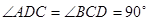
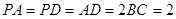 ,
,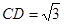 ,
,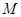 在棱
在棱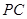 上,
上,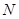 是
是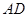 的中点,二面角
的中点,二面角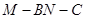 为
为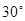 求
求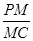 的值;
的值;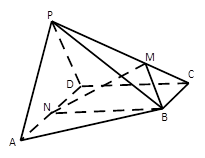
 的中位线
的中位线 ,将平面
,将平面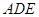 折起,平面
折起,平面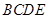 ,得到四棱锥
,得到四棱锥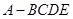 ,
,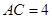 ,设
,设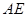 、
、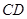 的中点分别为
的中点分别为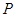 、
、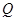 ,
,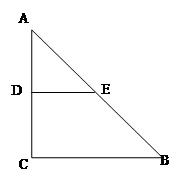

 满足
满足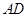 ∥
∥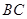 ,
,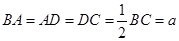 ,
,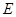 是
是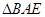 沿着
沿着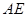 翻折成
翻折成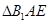 ,使面
,使面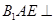 面
面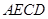 ,
, 为
为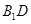 的中点.
的中点. 
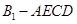 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: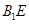 ∥面
∥面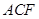 ;
;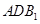 与面
与面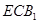 所成二面角的余弦值.
所成二面角的余弦值.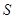 —
—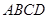 的底面
的底面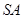 ⊥底面
⊥底面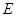 是
是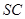 上的任意一点。
上的任意一点。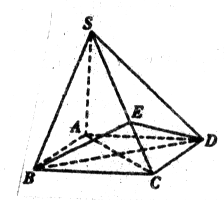

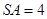 ,
,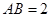 ,求点
,求点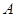 到平面的
到平面的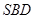 距离
距离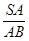 的值为多少时,二面角
的值为多少时,二面角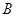 —
—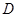 的大小为120°
的大小为120°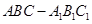 中,
中, 、
、 分别是
分别是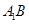 、
、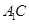 的中点,点
的中点,点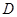 在
在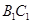 上,
上,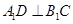 。
。 
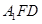
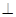 平面
平面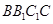 .
.