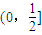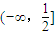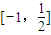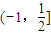题目内容
若变量x和y满足条件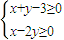 则t=2x+y的最小值为 ;z=
则t=2x+y的最小值为 ;z=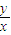 的取值范围是 .
的取值范围是 .
【答案】分析:先根据条件画出可行域,t=2x+y,z=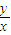 ,再利用几何意义求最值,只需求出直线t=2x+y的截距或可行域内的点与原点(0,0)连线的斜率的最值,从而得到z最值即可.
,再利用几何意义求最值,只需求出直线t=2x+y的截距或可行域内的点与原点(0,0)连线的斜率的最值,从而得到z最值即可.
解答:解:先根据约束条件画出可行域,
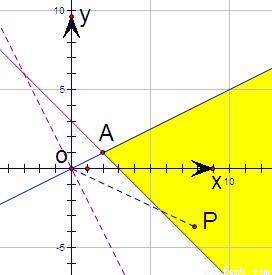
z=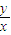 ,
,
∵可行域内点与原点(0,0)连线的斜率的最值,
当连线与直线x+y-3=0平行时,
z最大,最大值为1,
当连线与直线x-2y=0近似平行时,
z最小,最小值为 ,
,
∴z=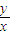 ∈
∈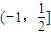
另外,当直线t=2x+y经过点A(2,1)时,t=2x+y的最小,最小值为5,
故填:5,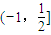 .
.
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.
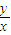 ,再利用几何意义求最值,只需求出直线t=2x+y的截距或可行域内的点与原点(0,0)连线的斜率的最值,从而得到z最值即可.
,再利用几何意义求最值,只需求出直线t=2x+y的截距或可行域内的点与原点(0,0)连线的斜率的最值,从而得到z最值即可.解答:解:先根据约束条件画出可行域,

z=
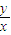 ,
,∵可行域内点与原点(0,0)连线的斜率的最值,
当连线与直线x+y-3=0平行时,
z最大,最大值为1,
当连线与直线x-2y=0近似平行时,
z最小,最小值为
 ,
,∴z=
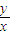 ∈
∈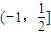
另外,当直线t=2x+y经过点A(2,1)时,t=2x+y的最小,最小值为5,
故填:5,
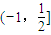 .
.点评:本题主要考查了简单的线性规划,以及利用几何意义求最值,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
若变量x和y满足条件
,则
的取值范围是( )
|
| y |
| x |
A、(0,
| ||
B、(-∞,
| ||
C、[-1,
| ||
D、(-1,
|
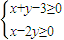 ,则
,则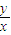 的取值范围是( )
的取值范围是( )