题目内容

如图所示，设P为△ABC所在平面内的一点，并且=+，则△ABP与△ABC的面积之比等于（ ）

A．
B．
C．
D．
【答案】分析：本题考查的知识点是向量在几何中的应用，及三角形面积的性质，由△ABP与△ABC为同底不等高的三角形，故高之比即为两个三角面积之间，连接CP并延长后，我们易得到CP与CD长度的关系，进行得到△ABP的面积与△ABC面积之比．
解答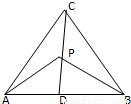：解：连接CP并延长交AB于D，
∵P、C、D三点共线，∴
AP
=λ
AD
+μ
AC
且λ+μ=1
设
AB
=k
AD
，结合
AP
=
1
5
AB
+
2
5
AC
得
AP
=
k
5
AD
+
2
5
AC
由平面向量基本定理解之，得λ=
3
5
，k=3且μ=
2
5
∴
AP
=
3
5
AD
+
2
5
AC
，可得
PD
=
2
5
CD
，
∵△ABP的面积与△ABC有相同的底边AB
高的比等于
|PD|
与
|CD|
之比
∴△ABP的面积与△ABC面积之比为
2
5
故选：C
点评：三角形面积性质：同（等）底同（等）高的三角形面积相等；同（等）底三角形面积这比等于高之比；同（等）高三角形面积之比等于底之比．
练习册系列答案
相关题目
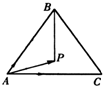精英家教网如图所示，设P为△ABC所在平面内的一点，并且
AP
=
1
5
AB
+
2
5
AC
，则△ABP与△ABC的面积之比等于（　　）
A、
1
5
B、
1
2
C、
2
5
D、
2
3
如图所示，设P为椭圆+=1(a＞b＞0)上一点，A为椭圆长轴右端点，若OP⊥PA，则椭圆离心率e的取值范围是________________.

（1）过一点向平面引垂线，________叫做这个点在这个平面内的射影；当这一点在平面内时，该点在平面上的射影就是它______；这一点与_______的线段叫做这点到这个平面的_______.如图所示，直线PQ⊥α,Q∈α,则点Q是______在平面α内的_____，线段_______是点_______到平面α的______.?

（2）一条直线和一个平面相交，但不______时，这条直线就叫做这个平面的_______，斜线与平面的交点叫做_____.从平面外一点向平面引斜线，这点与________间的线段叫做这点到这个平面的_______.如图所示，直线PR∩α=R,PR不______于α,直线PR是α的一条_____，点R为_______，线段_____是点P到α的______.?

（3）平面外一点到这个平面的垂线段______条，而这点到这个平面的______有无数条.?

（4）从斜线上斜足以外的一点向平面引垂线，过垂足的直线叫做斜线在这个平面内的_______，________与________间的线段叫做这点到平面的斜线段在这个平面内的________.如图所示，直线_____是直线PR在平面α上的______，线段______是点P到平面α的斜线段PR在平面α上的射影.?

（5）斜线上任意一点在平面上的射影一定在斜线的_____上.事实上，设a是平面α的斜线，B为斜足，在a上任取一点A，作AA1⊥α,A1是垂足，则A1、B确定的直线a′是a在平面α内的______，如图所示，设P是a上任意一点，在a和AA1确定的平面内，作PP1∥AA1,PP1必与a′相交于一点P1.∵AA1α__________ ,PP1______________AA1，∴PP1__________α.P1为P在平面α上的射影，所以点P在平面α上的射影一定在直线a在平面α上的射影a′上.

如图所示，设P为△ABC所在平面内的一点，并且=+，则△ABP与△ABC的面积之比等于（ ）

A．
B．
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网