Question

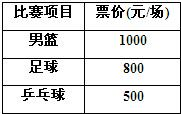
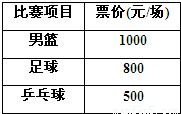
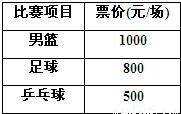
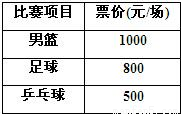
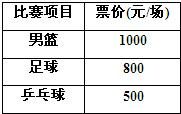2009年第十一届全国运动会在美丽的泉城济南胜利召开，下表为济南全运会官方票务网站公布的几种球类比赛的门票价格，某球迷赛前准备用12 000元预订15张下表中球类比赛的门票：
若在准备资金允许的范围内和总票数不变的前提下，该球迷想预订上表中三种球类比赛门票，其中足球比赛门票数与乒乓球比赛门票数相同，且足球比赛门票的费用不超过男篮比赛门票的费用，求可以预订的男篮比赛门票数．

Answer 1

分析：直接设出三种门票张数，根据不同票价以及总费用列出两个不等式，解出不等式组即可解决问题．

解答：解：设足球比赛门票数与乒乓球比赛门票数都预订n（n∈N^*）张，
则男篮比赛门票预订（15-2n）张，
得

800n+500n+1000(15-2n)≤12000 800n≤1000(15-2n)

，
解得4

2

7

≤n≤5

5

14

．由n∈N^*，可得n=5，
∴15-2n=5．
答：可以预订男篮比赛门票5张．

点评：本题考查实际问题的应用能力，以及一元一次不等式组的解法，“吃透”题意，理解题意是解决实际应用题的关键，本题属于基础题．