Question

已知函数.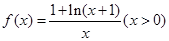

(1) 试判断函数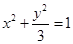在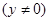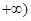上单调性并证明你的结论；

(2) 若恒成立, 求整数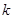的最大值；

(3) 求证：.

 

Answer 1

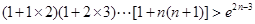【答案】

（1）上是减函数

（2）正整数k的最大值是3

（3）由(Ⅱ)知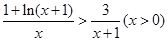∴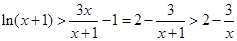利用放缩法得到。

【解析】

试题分析：解：(1)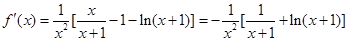

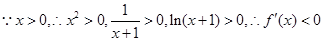
 上是减函数 4分

(2)即h(x)的最小值大于k.

 则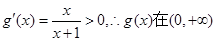上单调递增,

又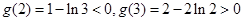 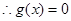存在唯一实根a, 且满足

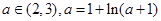
当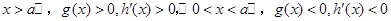 

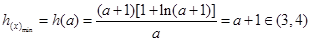∴ 故正整数k的最大值是3  ----9分

(3)由(Ⅱ)知∴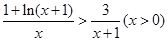 

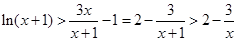
令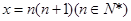, 则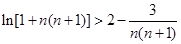

∴ln(1＋1×2)＋ln(1＋2×3)＋…＋ln[1＋n(n＋1)]

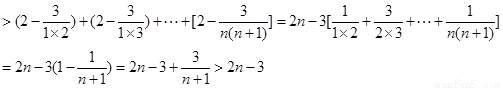
∴(1＋1×2)(1＋2×3)…[1＋n(n＋1)]＞e^2n－3          14分

考点：导数的运用

点评：主要是考查了导数在研究函数单调性的运用，属于中档题。