题目内容
16.一个人有5把钥匙,其中只有一把能打开他的房门,他随意地进行试开,并将试开不对的钥匙除去,则打开房门所试开次数ξ的数学期望为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 求出此人打开房门的概率,然后求解期望即可.
解答 解:由题意可知,此人第X次打开房门,则X的取值为1,2,3,4,5.
P(ξ=1)=$\frac{1}{5}$,
P(ξ=2)=$\frac{4×1}{5×4}$=$\frac{1}{5}$,
P(ξ=3)=$\frac{4×3×1}{5×4×3}$=$\frac{1}{5}$,
P(ξ=4)=$\frac{4×3×2×1}{5×4×3×2}$=$\frac{1}{5}$,
P(ξ=5)=$\frac{4×3×2×1×1}{5×4×3×2×1}$=$\frac{1}{5}$,
打开房门所试开次数ξ的数学期望为:Eξ=(1+2+3+4+5)×$\frac{1}{5}$=3.
故选:B.
点评 本题考查离散型随机变量的期望的求法,求解概率是解题的关键.

练习册系列答案
相关题目
8.已知f(x)=$\left\{\begin{array}{l}{{x}^{2}+2014x-2015,x≤0}\\{2-x+lnx,x>0}\end{array}\right.$,则函数f(x)的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.如图是一个几何体的三视图,其中正(主)视图、侧(左)视图都是矩形,则该几何体的体积是( )
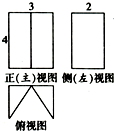

| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
6.有4名男医生、3名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
| A. | A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ | B. | C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | ||
| C. | C${\;}_{7}^{3}$--C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | D. | A${\;}_{7}^{3}$--A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ |