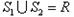题目内容
设S是实数集R的非空子集,如果?a,b∈S,有a+b∈S,a-b∈S,则称S是一个“和谐集”.下面命题为假命题的是( )
| A.存在有限集S,S是一个“和谐集” |
| B.对任意无理数a,集合{x|x=ka,k∈Z}都是“和谐集” |
| C.若S1≠S2,且S1,S2均是“和谐集”,则S1∩S2≠∅ |
| D.对任意两个“和谐集”S1,S2,若S1≠R,S2≠R,则S1∪S2=R |
A是真命题 S={0}是和谐集;
B是真命题:
设 x1=k1a,x2=k2a,k1,k2∈Z
x1+x2=(k1+k2)a∈S
x1-x2=(k1-k2)a∈S
∴S={x|x=ka,a是无理数,k∈Z)是和谐集
C是真命题:任意和谐集中一定含有0,
∴S1∩S2≠∅;
D假命题
取S1={x|x=2k,k∈Z},S2={x|x=3k,k∈Z∈}
S1,S2均是和谐集,但5不属于S1,也不属于S2
∴S1∪S2不是实数集.
故选D.
B是真命题:
设 x1=k1a,x2=k2a,k1,k2∈Z
x1+x2=(k1+k2)a∈S
x1-x2=(k1-k2)a∈S
∴S={x|x=ka,a是无理数,k∈Z)是和谐集
C是真命题:任意和谐集中一定含有0,
∴S1∩S2≠∅;
D假命题
取S1={x|x=2k,k∈Z},S2={x|x=3k,k∈Z∈}
S1,S2均是和谐集,但5不属于S1,也不属于S2
∴S1∪S2不是实数集.
故选D.

练习册系列答案
相关题目
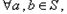 有a+b∈S,a-b∈S,则称S是一个“和谐集”。下面命题为假命题的是
有a+b∈S,a-b∈S,则称S是一个“和谐集”。下面命题为假命题的是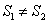 ,且
,且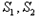 均是“和谐集”,则
均是“和谐集”,则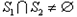
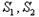 ,若
,若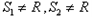 ,则
,则