题目内容
以O为原点,![]() 所在直线为
所在直线为![]() 轴,建立如 所示的坐标系。设
轴,建立如 所示的坐标系。设![]() ,点F的坐标为
,点F的坐标为![]() ,
,![]() ,点G的坐标为
,点G的坐标为![]() 。
。
(1)求![]() 关于
关于![]() 的函数
的函数![]() 的表达式,判断函数
的表达式,判断函数![]() 的单调性,并证明你的判断;
的单调性,并证明你的判断;
(2)设ΔOFG的面积![]() ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当![]() 取最小值时椭圆的方程;
取最小值时椭圆的方程;
(3)在(2)的条件下,若点P的坐标为![]() ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
(1)![]() 函数
函数![]() 在
在![]() 是单调递增函数。
是单调递增函数。
(2)椭圆方程为:![]()
(3)实数![]() 的取值范围为
的取值范围为![]() 。
。
解析:
(1)由题意知![]() ,则
,则![]()
函数![]() 在
在![]() 是单调递增函数。(证明略)(4分)
是单调递增函数。(证明略)(4分)
(2)由![]() ,
,
点G![]() ,
,
因![]() 在
在![]() 上是增函数,当
上是增函数,当![]() 时,
时,![]() 取最小值,此时
取最小值,此时![]() ,
,
依题意椭圆的中心在原点,一个焦点F(3,0),设椭圆方程为![]() ,由G点坐标代入与焦点F(3,0),可得椭圆方程为:
,由G点坐标代入与焦点F(3,0),可得椭圆方程为:![]() (9分)
(9分)
(3)设![]() ,则
,则![]() ,
,
由![]() ,
,![]() ,
,
因点C、D在椭圆上,代入椭圆方程得,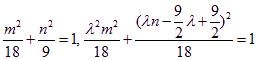 ,消去
,消去![]() ,
,
得![]() ,又
,又![]() ,
,
则实数![]() 的取值范围为
的取值范围为![]() 。
。

练习册系列答案
相关题目

 以O为原点,
以O为原点, 所在直线为x轴,建立如图所示的直角坐标系.若
所在直线为x轴,建立如图所示的直角坐标系.若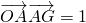 ,点A的坐标为(t,0),t∈(0,+∞),点G的坐标为(m,3).
,点A的坐标为(t,0),t∈(0,+∞),点G的坐标为(m,3).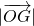 取最小值时双曲线C的方程;
取最小值时双曲线C的方程; 所在直线为x轴,建立直角坐标系.设
所在直线为x轴,建立直角坐标系.设 ,点F的坐标为(t,0),t∈[3,+∞).点G的坐标为(x,y).
,点F的坐标为(t,0),t∈[3,+∞).点G的坐标为(x,y). ,若O以为中心,F,为焦点的椭圆经过点G,求当
,若O以为中心,F,为焦点的椭圆经过点G,求当 取最小值时椭圆的方程.
取最小值时椭圆的方程. ,C,D是椭圆上的两点,
,C,D是椭圆上的两点, ,求实数λ的取值范围.
,求实数λ的取值范围.