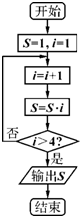
题目内容
(12分)某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生
(I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
|
运行次数n |
输出y的值为1的频数 |
输出y的值为2的频数 |
输出y的值为3的频数 |
|
30 |
14 |
6 |
10 |
|
… |
… |
… |
… |
|
2100 |
1027 |
376 |
697 |
乙的频数统计图(部分)
|
运行次数n |
输出y的值为1的频数 |
输出y的值为2的频数 |
输出y的值为3的频数 |
|
30 |
12 |
11 |
7 |
|
… |
… |
… |
… |
|
2100 |
1051 |
696 |
353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合要求的可能系较大;
(III)将按程序摆图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.

(I)输出的y值为1的概率为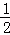 ,输出的y值为2的概率为
,输出的y值为2的概率为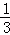 ,输出的y值为3的概率为
,输出的y值为3的概率为
(II)乙同学所编程序符合算法要求的可能性较大(III)1
【解析】(I)变量x是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能,
当x从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出的y值为1,故P1=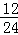 =
=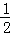 ;
;
当x从2,4,8,10,14,16,20,22这8个数中产生时,输出的y值为2,故P2=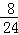 =
=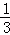 ;
;
当x从6,12,18,24这4个数中产生时,输出的y值为3,故P3=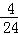 =
= ;
;
故输出的y值为1的概率为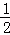 ,输出的y值为2的概率为
,输出的y值为2的概率为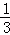 ,输出的y值为3的概率为
,输出的y值为3的概率为 ;
;
(II)当n=2100时,甲、乙所编程序各自输出的y值为i(i=1,2,3)的频率如下:
|
|
输出y值为1的频率 |
输出y值为2的频率 |
输出y值为3的频率 |
|
甲 |
|
|
|
|
乙 |
|
|
|
比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大;
(III)随机变量ξ的可能取值为:0,1,2,3,P(ξ=0)=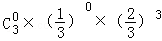 =
=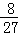 ,P(ξ=1)=
,P(ξ=1)= =
=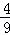
P(ξ=2)=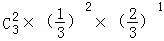 =
=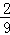 ,P(ξ=3)=
,P(ξ=3)=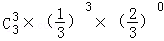 =
=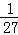 ,故ξ的分布列为:
,故ξ的分布列为:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
所以所求的数学期望Eξ=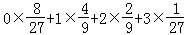 =1
=1

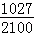
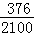

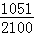
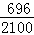
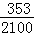
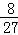
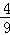
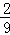
 4、某算法的程序框图如图,若输入a=4,b=2,c=6,则输出的结果为
4、某算法的程序框图如图,若输入a=4,b=2,c=6,则输出的结果为 (2013•成都二模)某算法的程序框图如图所示,则执行该程序后输出的S等于( )
(2013•成都二模)某算法的程序框图如图所示,则执行该程序后输出的S等于( ) 某算法的程序框图如图所示,则输出的S的值为
某算法的程序框图如图所示,则输出的S的值为 已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…(xn,yn),…
已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…(xn,yn),…