题目内容
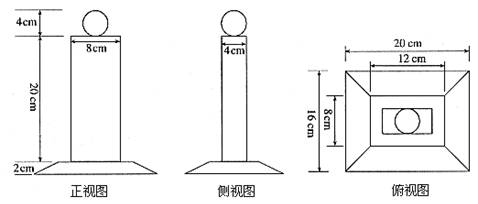
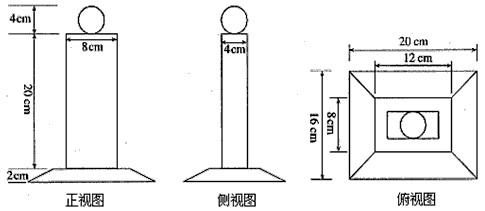
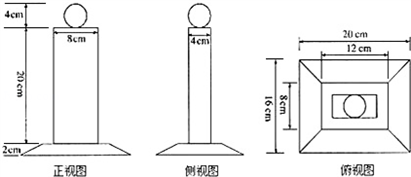
如图,这是一个奖杯的三视图,(1)请你说明这个奖杯是由哪些基本几何体组成的;(2)求出这个奖杯的体积.

【答案】分析:(1)根据已知中的三视图,我们可知该几何体有三部分组成,分析三部分三视图,进而分析出三部分的形状,即可得到答案.
(2)根据(1)中分析的几何体的形状,结合球、棱柱及棱台的体积公式,即可算出这个奖杯的体积.
解答:解:(1)该奖杯有三部分组成,
由于上部的三视图均为圆,故上部为一个球;
中部的三视图均为矩形,故中部为一个直四棱柱;
下部的三视图有两个为梯形,一个为正方形,故下部为一个四棱台;
该奖杯由一个球、一个直四棱柱、一个四棱台组成.(4分)
(2)由三视图可知,球的直径为4cm;
直四棱柱的高为20cm,底面长为8cm,底面宽为4cm;
四棱台的高为2cm,上底面长为12cm、宽为8cm,下底面长为20cm、宽为16cm.(8分)
所以,所求奖杯的体积为
V=V球+V直四棱柱+V四棱台=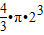 +8×4×20+
+8×4×20+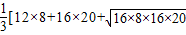 ]×2(12分)
]×2(12分)
点评:本题考查的知识点是组合几何体的面积、体积其中根据已知中的三视图判断出组合体各组成部分的形状及棱长,半径等几何量是解答的关键.
(2)根据(1)中分析的几何体的形状,结合球、棱柱及棱台的体积公式,即可算出这个奖杯的体积.
解答:解:(1)该奖杯有三部分组成,
由于上部的三视图均为圆,故上部为一个球;
中部的三视图均为矩形,故中部为一个直四棱柱;
下部的三视图有两个为梯形,一个为正方形,故下部为一个四棱台;
该奖杯由一个球、一个直四棱柱、一个四棱台组成.(4分)
(2)由三视图可知,球的直径为4cm;
直四棱柱的高为20cm,底面长为8cm,底面宽为4cm;
四棱台的高为2cm,上底面长为12cm、宽为8cm,下底面长为20cm、宽为16cm.(8分)
所以,所求奖杯的体积为
V=V球+V直四棱柱+V四棱台=
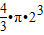 +8×4×20+
+8×4×20+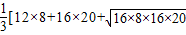 ]×2(12分)
]×2(12分)点评:本题考查的知识点是组合几何体的面积、体积其中根据已知中的三视图判断出组合体各组成部分的形状及棱长,半径等几何量是解答的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
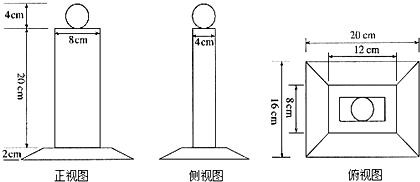 如图,这是一个奖杯的三视图,(1)请你说明这个奖杯是由哪些基本几何体组成的;
如图,这是一个奖杯的三视图,(1)请你说明这个奖杯是由哪些基本几何体组成的;