题目内容
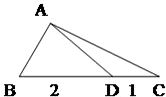 △ABC中,D在边BC上,且BD=2,DC=1,∠B=60°,∠ADC=150°,求AC的长及△ABC的面积.
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60°,∠ADC=150°,求AC的长及△ABC的面积.
分析:∠BAD=150°-60°=90°,可得 AD=2sin60°=
,余弦定理求出AC,利用直角三角形中的边角关系求出AB,利用
AB×BDsin∠B 求出△ABC的面积.
| 3 |
| 1 |
| 2 |
解答:解:在△ABC中,∠BAD=150°-60°=90°,∴AD=2sin60°=
.
在△ACD中,AC2=(
)2+12-2×
×1×cos150°=7,∴AC=
.
∴AB=2cos60°=1,S△ABC=
×1×3×sin60°=
.
| 3 |
在△ACD中,AC2=(
| 3 |
| 3 |
| 7 |
∴AB=2cos60°=1,S△ABC=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查直角三角形中的边角关系,余弦定理的应用,求出AD的值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
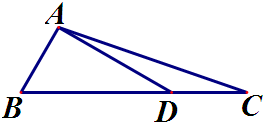 如图所示在△ABC中,D在边BC上,且BD=2,DC=1,∠B=60°,∠ADB=30°,求AC的长及△ABC的面积.
如图所示在△ABC中,D在边BC上,且BD=2,DC=1,∠B=60°,∠ADB=30°,求AC的长及△ABC的面积.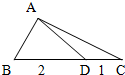 △ABC中,D在边BC上,且BD=2,DC=1,∠B=60°,∠ADC=150°,则AC=
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60°,∠ADC=150°,则AC=