题目内容
已知函数f(x)=| 1 | 3 |
(1)试用含a的代数式表示b,并求f(x)的单调区间;
(2)令a=-1,设函数f(x)在x1,x2(x1<x2)处取得极值,记点M (x1,f(x1)),N(x2,f(x2)),P(m,f(m)),x1<m<x2,请仔细观察曲线f(x)在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
(Ⅰ)若对任意的t∈(x1,x2),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
(Ⅱ)若存在点Q(n,f(n)),x≤n<m,使得线段PQ与曲线f(x)有异于P、Q的公共点,请直接写出m的取值范围(不必给出求解过程).
分析:(1)欲求:“f(x)的单调区间”,对于三次函数而言,利用导数解决,本题还得对字母a进行讨论;
(2)存在性问题,结合观察f(x)的图象,帮助分析问题.
(2)存在性问题,结合观察f(x)的图象,帮助分析问题.
解答:解:(1)依题意,得f′(x)=x2+2ax+b,
由f′(-1)=1-2a+b=0得b=2a-1
从而f(x)=
x3+ax2+(2a-1)x,
故f′(x)=(x+1)(x+2a-1)
令f′(x)=0,得x=-1或x=1-2a
①当a>1时,1-2a<-1
当x变化时,根据f′(x)与f(x)的变化情况得,
函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),单调减区间为(1-2a,-1)
②当a=1时,1-2a=-1,此时有f′(x)≥0恒成立,且仅在x=-1处f′(x)=0,故函数f(x)的单调增区间为R、
③当a<1时,1-2a>-1,同理可得,函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),
单调减区间为(-1,1-2a)
综上:当a>1时,函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),单调减区间为(1-2a,-1);
当a=1时,函数f(x)的单调增区间为R;
当a<1时,函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),单调减区间为(-1,1-2a)
(2)(Ⅰ)由a=-1得f(x)=
x3-x2-3x
令f′(x)=x2-2x-3=0得x1=-1,x2=3
由(1)得f(x)增区间为(-∞,-1)和(3,+∞),单调减区间为(-1,3),
所以函数f(x)在处x1=-1,x2=3处取得极值,故M(-1,
),N(3,-9)
观察f(x)的图象,有如下现象:
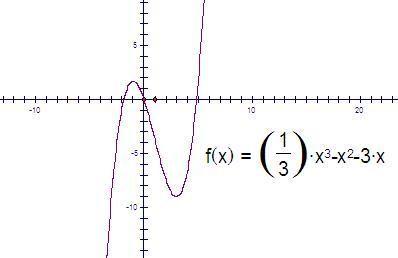
①当m从-1(不含-1)变化到3时,线段MP的斜率与曲线f(x)在点P处切线的斜率f(x)之差Kmp-f′(m)的值由正连续变为负、
②线段MP与曲线是否有异于H,P的公共点与Kmp-f′(m)的m正负有着密切的关联;
③Kmp-f′(m)=0对应的位置可能是临界点,故推测:满足Kmp-f′(m)的m就是所求的t最小值,下面给出证明并确定的t最小值、曲线f(x)在点P(m,f(m))处的切线斜率f′(m)=m2-2m-3;
线段MP的斜率Kmp=
,
当Kmp-f′(m)=0时,解得m=-1或m=2,
直线MP的方程为y=(
x+
),
令g(x)=f(x)-(
x+
),
当m=2时,g′(x)=x2-2x在(-1,2)上只有一个零点x=0,可判断f(x)函数在(-1,0)上单调递增,在(0,2)上单调递减,又g(-1)=g(2)=0,所以g(x)在(-1,2)上没有零点,即线段MP与曲线f(x)没有异于M,P的公共点、
当m∈(2,3]时,g(0)=-
>0,
g(2)=-(m-2)2<0,
所以存在δ∈(0,2]使得g(δ)=0,
即当m∈(2,3]时,MP与曲线f(x)有异于M,P的公共点
综上,t的最小值为2.
(Ⅱ)类似(1)于中的观察,可得m的取值范围为(1,3].
由f′(-1)=1-2a+b=0得b=2a-1
从而f(x)=
| 1 |
| 3 |
故f′(x)=(x+1)(x+2a-1)
令f′(x)=0,得x=-1或x=1-2a
①当a>1时,1-2a<-1
当x变化时,根据f′(x)与f(x)的变化情况得,
函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),单调减区间为(1-2a,-1)
②当a=1时,1-2a=-1,此时有f′(x)≥0恒成立,且仅在x=-1处f′(x)=0,故函数f(x)的单调增区间为R、
③当a<1时,1-2a>-1,同理可得,函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),
单调减区间为(-1,1-2a)
综上:当a>1时,函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),单调减区间为(1-2a,-1);
当a=1时,函数f(x)的单调增区间为R;
当a<1时,函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),单调减区间为(-1,1-2a)
(2)(Ⅰ)由a=-1得f(x)=
| 1 |
| 3 |
令f′(x)=x2-2x-3=0得x1=-1,x2=3
由(1)得f(x)增区间为(-∞,-1)和(3,+∞),单调减区间为(-1,3),
所以函数f(x)在处x1=-1,x2=3处取得极值,故M(-1,
| 5 |
| 3 |
观察f(x)的图象,有如下现象:

①当m从-1(不含-1)变化到3时,线段MP的斜率与曲线f(x)在点P处切线的斜率f(x)之差Kmp-f′(m)的值由正连续变为负、
②线段MP与曲线是否有异于H,P的公共点与Kmp-f′(m)的m正负有着密切的关联;
③Kmp-f′(m)=0对应的位置可能是临界点,故推测:满足Kmp-f′(m)的m就是所求的t最小值,下面给出证明并确定的t最小值、曲线f(x)在点P(m,f(m))处的切线斜率f′(m)=m2-2m-3;
线段MP的斜率Kmp=
| m2-4m-5 |
| 3 |
当Kmp-f′(m)=0时,解得m=-1或m=2,
直线MP的方程为y=(
| m2-4m-5 |
| 3 |
| m2- 4m |
| 3 |
令g(x)=f(x)-(
| m2-4m-5 |
| 3 |
| m2- 4m |
| 3 |
当m=2时,g′(x)=x2-2x在(-1,2)上只有一个零点x=0,可判断f(x)函数在(-1,0)上单调递增,在(0,2)上单调递减,又g(-1)=g(2)=0,所以g(x)在(-1,2)上没有零点,即线段MP与曲线f(x)没有异于M,P的公共点、
当m∈(2,3]时,g(0)=-
| m2-4m |
| 3 |
g(2)=-(m-2)2<0,
所以存在δ∈(0,2]使得g(δ)=0,
即当m∈(2,3]时,MP与曲线f(x)有异于M,P的公共点
综上,t的最小值为2.
(Ⅱ)类似(1)于中的观察,可得m的取值范围为(1,3].
点评:本题综合考查了函数导数的综合应用,本题是函数的综合题,综合考查了利用导数求函数的单调区间,求函数的极值,以及存在性问题,有一定的难度,是一道很好的压轴题.

练习册系列答案
相关题目
已知函数f(x)=
,g(x)=1+
,若f(x)>g(x),则实数x的取值范围是( )
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、(-∞,-1)∪(0,1) | ||||
B、(-∞,-1)∪(0,
| ||||
C、(-1,0)∪(
| ||||
D、(-1,0)∪(0,
|