题目内容
在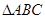 中,“
中,“ ”是“
”是“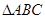 为直角三角形”的
为直角三角形”的
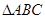 中,“
中,“ ”是“
”是“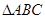 为直角三角形”的
为直角三角形”的| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分又不必要条件 |
A
分析:先证明充分性,设
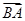 与
与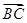 的夹角为α,利用平面向量的数量积运算法则化简
的夹角为α,利用平面向量的数量积运算法则化简 ?
? 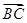 ,由已知
,由已知 ?
? 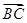 =0,得到cosα值为0,由α的范围,利用特殊角的三角函数值求出α为直角,可得三角形ABC为直角三角形;反过来,若三角形ABC为直角三角形,但不一定B为直角,故必要性不一定成立.
=0,得到cosα值为0,由α的范围,利用特殊角的三角函数值求出α为直角,可得三角形ABC为直角三角形;反过来,若三角形ABC为直角三角形,但不一定B为直角,故必要性不一定成立.解:当
 ?
? 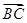 =0时,
=0时,设
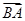 与
与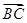 的夹角为α,
的夹角为α,可得
 ?
? 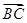 =ac?cos(π-α)=-ac?cosα,
=ac?cos(π-α)=-ac?cosα,又
 ?
? 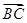 =0,
=0,∴-ac?cosα=0,即cosα=0,
∵α∈(0,π)
∴α=
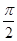 ,
,则△ABC为直角三角形;
而当△ABC为直角三角形时,B不一定为直角,
故
 ?
? 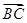 不一定等于0,
不一定等于0,则在△ABC中,“
 ?
? 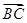 =0”是“△ABC为直角三角形”的充分不必要条件.
=0”是“△ABC为直角三角形”的充分不必要条件.故选A

练习册系列答案
相关题目

 距A处8处有一走私船,正沿东偏南
距A处8处有一走私船,正沿东偏南 的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以
的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以 海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇航行方向。
海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇航行方向。

 ,求实数m的值。
,求实数m的值。 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知
 求
求 的值。
的值。 中,∠A:∠B=1:2,∠
中,∠A:∠B=1:2,∠ 的平分线
的平分线 分⊿ACD与⊿BCD的面积比是3:2,
分⊿ACD与⊿BCD的面积比是3:2,
 中,角A,B,C所对应的边分别为
中,角A,B,C所对应的边分别为 ,则角A的大小为
,则角A的大小为  中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
,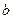 ,
, ,
, 为
为 ,
, 满足
满足
 ∥
∥ ,则角
,则角 .
. (
( 为非零实数),
为非零实数), 则
则 ( )
( )