题目内容
已知幂函数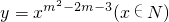 的图象关于y轴对称,且在(0,+∞)上是减函数,则满足
的图象关于y轴对称,且在(0,+∞)上是减函数,则满足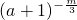 <
<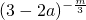 的a的范围是________.
的a的范围是________.
(-∞,-1)∪( ,
, )
)
分析:(1)幂函数y=xα的图象关于y轴对称,且在(0,+∞)上是减函数.则必须满足α为偶数且α<0,由此可得m的值.
(2)根据幂函数y=xα的单调性,可得a+1>3-2a>0,或0>a+1>3-2a,或a+1<0<3-2a,先求得每个不等式的解集,再取并集.即得所求.
解答:∵幂函数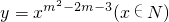 的图象关于y轴对称,故此函数为偶函数,故有m2-2m-3为偶数,
的图象关于y轴对称,故此函数为偶函数,故有m2-2m-3为偶数,
∵函数在(0,+∞)上递减,∴m2-2m-3<0,即-1<m<3,又m∈N*,∴m=1.
∵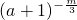 <
<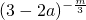 ,且函数y=
,且函数y=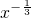 在(-∞,0),(0,+∞)上都是减函数,
在(-∞,0),(0,+∞)上都是减函数,
故有 a+1>3-2a>0,或0>a+1>3-2a,或a+1<0<3-2a,
解得a<-1,或 <a<
<a< ,
,
故答案为 (-∞,-1)∪( ,
, ).
).
点评:幂函数y=xα,α<0时则为减函数;α>0时,幂函数为增函数.要注意α的不同,其定义域是不同的,解不等式时要注意,属于基础题.
 ,
, )
)分析:(1)幂函数y=xα的图象关于y轴对称,且在(0,+∞)上是减函数.则必须满足α为偶数且α<0,由此可得m的值.
(2)根据幂函数y=xα的单调性,可得a+1>3-2a>0,或0>a+1>3-2a,或a+1<0<3-2a,先求得每个不等式的解集,再取并集.即得所求.
解答:∵幂函数
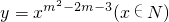 的图象关于y轴对称,故此函数为偶函数,故有m2-2m-3为偶数,
的图象关于y轴对称,故此函数为偶函数,故有m2-2m-3为偶数,∵函数在(0,+∞)上递减,∴m2-2m-3<0,即-1<m<3,又m∈N*,∴m=1.
∵
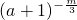 <
<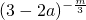 ,且函数y=
,且函数y=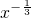 在(-∞,0),(0,+∞)上都是减函数,
在(-∞,0),(0,+∞)上都是减函数,故有 a+1>3-2a>0,或0>a+1>3-2a,或a+1<0<3-2a,
解得a<-1,或
 <a<
<a< ,
,故答案为 (-∞,-1)∪(
 ,
, ).
).点评:幂函数y=xα,α<0时则为减函数;α>0时,幂函数为增函数.要注意α的不同,其定义域是不同的,解不等式时要注意,属于基础题.

练习册系列答案
相关题目
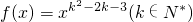 的图象关于y轴对称,且在区间(0,+∞)上是减函数,
的图象关于y轴对称,且在区间(0,+∞)上是减函数, 的图象关于
的图象关于 轴对称,且在区间
轴对称,且在区间 上是减函数,
上是减函数, 的解析式;((2)若
的解析式;((2)若 ,比较
,比较 与
与 的大小;
的大小;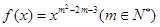 的图象关于
的图象关于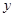 轴对称,且在
轴对称,且在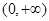 上是减函数,则
上是减函数,则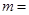 _____________________.
_____________________. 的图象关于y轴对称,且在(0,+∞)上是减函数,则m= .
的图象关于y轴对称,且在(0,+∞)上是减函数,则m= .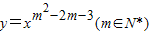 的图象关于y轴对称,且在(0,+∞)上是减函数.
的图象关于y轴对称,且在(0,+∞)上是减函数.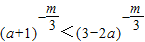 的a的取值范围.
的a的取值范围.