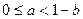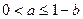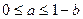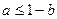题目内容
设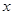 、
、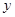 满足约束条件
满足约束条件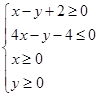 ,若目标函数
,若目标函数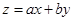
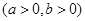 的最大值为6,则
的最大值为6,则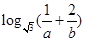 的最小值为
的最小值为
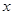 、
、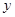 满足约束条件
满足约束条件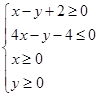 ,若目标函数
,若目标函数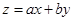
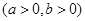 的最大值为6,则
的最大值为6,则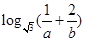 的最小值为
的最小值为A.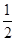 | B.3 | C.2 | D.4 |
C
本题考查纯线性规划及函数的最值
首先作出满足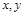 的可行域,如图中的阴影所示,其中
的可行域,如图中的阴影所示,其中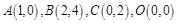
因为 ,所以目标函数
,所以目标函数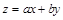 表示直线
表示直线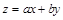 在轴
在轴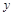 上的截距,直线
上的截距,直线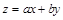 在
在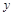 上的截距取得最大值时,目标函数
上的截距取得最大值时,目标函数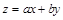 也取得最大值
也取得最大值
因为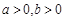 ,所以直线
,所以直线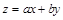 的斜率
的斜率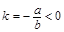
作初始直线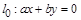 并将直线
并将直线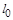 在可行域内平移,可知当直线
在可行域内平移,可知当直线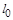 过点
过点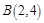 时目标函数
时目标函数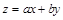 取得最大值
取得最大值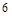
即有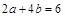
所有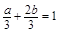
所以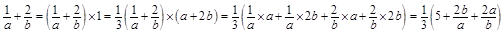
因为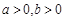 ,由均值不等式定理得
,由均值不等式定理得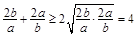 ,其中当且仅当
,其中当且仅当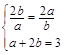 ,即
,即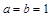 时取等号成立,所以
时取等号成立,所以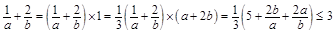
所以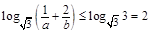
 故正确答案为C
故正确答案为C
首先作出满足
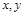 的可行域,如图中的阴影所示,其中
的可行域,如图中的阴影所示,其中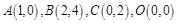
因为
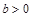 ,所以目标函数
,所以目标函数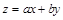 表示直线
表示直线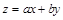 在轴
在轴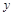 上的截距,直线
上的截距,直线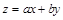 在
在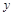 上的截距取得最大值时,目标函数
上的截距取得最大值时,目标函数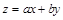 也取得最大值
也取得最大值因为
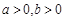 ,所以直线
,所以直线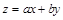 的斜率
的斜率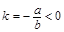
作初始直线
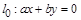 并将直线
并将直线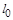 在可行域内平移,可知当直线
在可行域内平移,可知当直线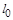 过点
过点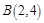 时目标函数
时目标函数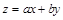 取得最大值
取得最大值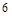
即有
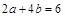
所有
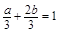
所以
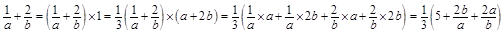
因为
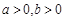 ,由均值不等式定理得
,由均值不等式定理得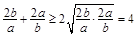 ,其中当且仅当
,其中当且仅当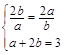 ,即
,即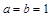 时取等号成立,所以
时取等号成立,所以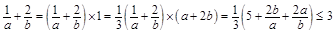
所以
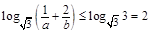
 故正确答案为C
故正确答案为C
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
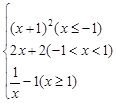 ,已知f(a)>1,则a的取值范围是( )
,已知f(a)>1,则a的取值范围是( )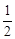 ,+∞)
,+∞) .
.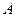 、
、 ,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表:
,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表: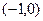 与点
与点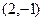 分别位于直线
分别位于直线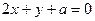 的两侧,则实数
的两侧,则实数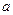 的取值范围是_.
的取值范围是_.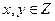 ,
,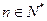 ,设
,设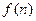 是不等式组
是不等式组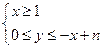 ,表示的平面区域内可行解的个数,
,表示的平面区域内可行解的个数, 由此
由此 可推出
可推出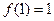 ,
, ,……, 则
,……, 则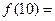 ( )
( )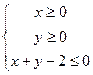 所围成的区域面积为_
所围成的区域面积为_  ▲ ____
▲ ____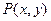 的坐标满足
的坐标满足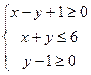 ,设A(2,1), 则
,设A(2,1), 则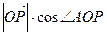 (
( 为坐标原点)的最大值为
为坐标原点)的最大值为 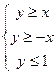 表示的平面区域为
表示的平面区域为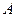 ,不等式
,不等式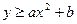 (
(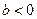 ,
,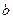 为常数)表示的平面区域为
为常数)表示的平面区域为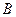 ,
,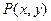 为平面上任意一点,
为平面上任意一点,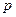 :点
:点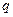 :点
:点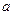 的取值范围是
的取值范围是