题目内容
已知函数
(1)若函数 在x=1处的切线l与直线y=4x+3平行,求实数a的值;
(2)若函数f(x)在(2,+∞)上存在单调递增区间,求实数a的取值范围;
(3)在(1)的条件下,设函数 ,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,求实数m的取值范围.
,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,求实数m的取值范围.
解:(1)求导函数f′(x)=ax2+2x-1
∵函数在x=1处的切线l与直线y=4x+3平行,
∴f′(1)=a+1=4
∴a=3
(2)求导函数f′(x)=ax2+2x-1,函数f(x)在(2,+∞)上存在单调递增区间,只需f′(x)=ax2+2x-1>0在(2,+∞)上有解即可
f′(x)=ax2+2x-1>0在(2,+∞)上有解,即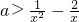 在(2,+∞)上有解
在(2,+∞)上有解
∵
∴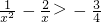
∴
∴实数a的取值范围是
(3)函数 ,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,只需要g(x)的图象y=m有两个不同的交点
,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,只需要g(x)的图象y=m有两个不同的交点
当x≥1时,g(x)=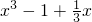 ,g′(x)=
,g′(x)= >0,函数g(x)单调递增
>0,函数g(x)单调递增
当x<1时,g(x)= ,g′(x)=-
,g′(x)=- =
=
令g′(x)>0,可得 <x
<x ,令g′(x)<0,可得x<
,令g′(x)<0,可得x< ,或x
,或x ,
,
∴函数在 上单调减,(-
上单调减,(- ,
, )上单调增,
)上单调增, 上单调减,(1,2)上单调增
上单调减,(1,2)上单调增
∴当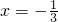 时,g(x)取得极小值
时,g(x)取得极小值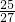 .当
.当 时,g(x)取得极大值
时,g(x)取得极大值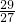 .g(-2)=
.g(-2)=
∴ 或
或 时,g(x)的图象y=m有两个不同的交点,方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根
时,g(x)的图象y=m有两个不同的交点,方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根
∴实数m的取值范围为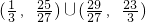 .
.
分析:(1)求导函数,利用导数的几何意义,结合函数在x=1处的切线l与直线y=4x+3平行,可实数a的值;
(2)求导函数f′(x)=ax2+2x-1,函数f(x)在(2,+∞)上存在单调递增区间,只需f′(x)=ax2+2x-1>0在(2,+∞)上有解即可;
(3)函数 ,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,只需要g(x)的图象y=m有两个不同的交点.
,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,只需要g(x)的图象y=m有两个不同的交点.
点评:本题重点考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查利用导数研究函数的图象,综合性强.
∵函数在x=1处的切线l与直线y=4x+3平行,
∴f′(1)=a+1=4
∴a=3
(2)求导函数f′(x)=ax2+2x-1,函数f(x)在(2,+∞)上存在单调递增区间,只需f′(x)=ax2+2x-1>0在(2,+∞)上有解即可
f′(x)=ax2+2x-1>0在(2,+∞)上有解,即
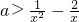 在(2,+∞)上有解
在(2,+∞)上有解∵

∴
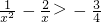
∴

∴实数a的取值范围是

(3)函数
 ,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,只需要g(x)的图象y=m有两个不同的交点
,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,只需要g(x)的图象y=m有两个不同的交点当x≥1时,g(x)=
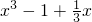 ,g′(x)=
,g′(x)= >0,函数g(x)单调递增
>0,函数g(x)单调递增当x<1时,g(x)=
 ,g′(x)=-
,g′(x)=- =
=
令g′(x)>0,可得
 <x
<x ,令g′(x)<0,可得x<
,令g′(x)<0,可得x< ,或x
,或x ,
,∴函数在
 上单调减,(-
上单调减,(- ,
, )上单调增,
)上单调增, 上单调减,(1,2)上单调增
上单调减,(1,2)上单调增∴当
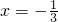 时,g(x)取得极小值
时,g(x)取得极小值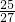 .当
.当 时,g(x)取得极大值
时,g(x)取得极大值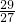 .g(-2)=
.g(-2)=
∴
 或
或 时,g(x)的图象y=m有两个不同的交点,方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根
时,g(x)的图象y=m有两个不同的交点,方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根∴实数m的取值范围为
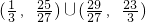 .
.分析:(1)求导函数,利用导数的几何意义,结合函数在x=1处的切线l与直线y=4x+3平行,可实数a的值;
(2)求导函数f′(x)=ax2+2x-1,函数f(x)在(2,+∞)上存在单调递增区间,只需f′(x)=ax2+2x-1>0在(2,+∞)上有解即可;
(3)函数
 ,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,只需要g(x)的图象y=m有两个不同的交点.
,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,只需要g(x)的图象y=m有两个不同的交点.点评:本题重点考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查利用导数研究函数的图象,综合性强.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围; .
.