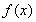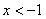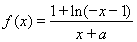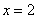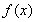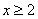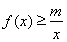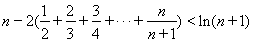题目内容
如果![]() 是函数
是函数![]() 的一个极值,称点
的一个极值,称点![]() 是函数
是函数![]() 的一个极值点.已知函数
的一个极值点.已知函数![]()
(1)若函数![]() 总存在有两个极值点
总存在有两个极值点![]() ,求
,求![]() 所满足的关系;
所满足的关系;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,且存在
,且存在![]() ,求
,求![]() 在不等式
在不等式![]() 表示的区域内时实数
表示的区域内时实数![]() 的范围.
的范围.
(3)若函数![]() 恰有一个极值点
恰有一个极值点![]() ,且存在
,且存在![]() ,使
,使![]() 在不等式
在不等式![]() 表示的区域内,证明:
表示的区域内,证明:![]() .
.
解析:(1)![]()
令![]() 得
得![]()
![]() 又
又 ![]()
![]() ………………3分
………………3分
(2)![]() 在
在![]() 有两个不相等的实根.
有两个不相等的实根.
即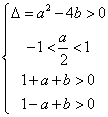 得
得 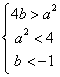
![]() ………………7分
………………7分
(3)由①![]()
![]()
①当![]() 在
在![]() 左右两边异号
左右两边异号
![]() 是
是![]() 的唯一的一个极值点
的唯一的一个极值点
由题意知![]() 即
即  即
即 ![]()
存在这样的![]() 的满足题意
的满足题意 ![]() 符合题意 ………………9分
符合题意 ………………9分
②当![]() 时,
时,![]() 即
即![]()
这里函数![]() 唯一的一个极值点为
唯一的一个极值点为![]()
由题意
即 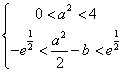 即
即 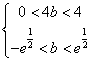
![]() ………………………………13分
………………………………13分
综上知:满足题意 ![]() 的范围为
的范围为![]() . ……………………………14分
. ……………………………14分

练习册系列答案
相关题目