题目内容
已知定义域为R的单调函数f(x)是奇函数,当x>0时, .
.(1)求f(x)的解析式;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求实数k的取值范围.
【答案】分析:(1)由定义域为R的函数f(x)是奇函数,知f(0)=0.当x<0时, ,由函数f(x)是奇函数,知
,由函数f(x)是奇函数,知 ,由此能求出f(x)的解析式.
,由此能求出f(x)的解析式.
(2)由 且f(x)在R上单调,知f(x)在R上单调递减,由f(t2-2t)+f(2t2-k)<0,得f(t2-2t)<-f(2t2-k),再由根的差别式能求出实数k的取值范围.
且f(x)在R上单调,知f(x)在R上单调递减,由f(t2-2t)+f(2t2-k)<0,得f(t2-2t)<-f(2t2-k),再由根的差别式能求出实数k的取值范围.
解答:解:(1)∵定义域为R的函数f(x)是奇函数,
∴f(0)=0,
当x<0时,-x>0,
 ,
,
又∵函数f(x)是奇函数,
∴f(-x)=-f(x),
∴ ,
,
综上所述 .
.
(2)∵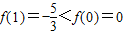 ,
,
且f(x)在R上单调,
∴f(x)在R上单调递减,
由f(t2-2t)+f(2t2-k)<0,
得f(t2-2t)<-f(2t2-k),
∵f(x)是奇函数,
∴f(t2-2t)<f(k-2t2),
又∵f(x)是减函数,
∴t2-2t>k-2t2
即3t2-2t-k>0对任意t∈R恒成立,
∴△=4+12k<0得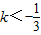 即为所求.
即为所求.
点评:本题考查函数的恒成立问题,解题时要认真审题,仔细解答,注意合理地进行等价转化,同时注意函数性质的灵活运用.
 ,由函数f(x)是奇函数,知
,由函数f(x)是奇函数,知 ,由此能求出f(x)的解析式.
,由此能求出f(x)的解析式.(2)由
 且f(x)在R上单调,知f(x)在R上单调递减,由f(t2-2t)+f(2t2-k)<0,得f(t2-2t)<-f(2t2-k),再由根的差别式能求出实数k的取值范围.
且f(x)在R上单调,知f(x)在R上单调递减,由f(t2-2t)+f(2t2-k)<0,得f(t2-2t)<-f(2t2-k),再由根的差别式能求出实数k的取值范围.解答:解:(1)∵定义域为R的函数f(x)是奇函数,
∴f(0)=0,
当x<0时,-x>0,
 ,
,又∵函数f(x)是奇函数,
∴f(-x)=-f(x),
∴
 ,
,综上所述
 .
.(2)∵
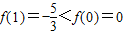 ,
,且f(x)在R上单调,
∴f(x)在R上单调递减,
由f(t2-2t)+f(2t2-k)<0,
得f(t2-2t)<-f(2t2-k),
∵f(x)是奇函数,
∴f(t2-2t)<f(k-2t2),
又∵f(x)是减函数,
∴t2-2t>k-2t2
即3t2-2t-k>0对任意t∈R恒成立,
∴△=4+12k<0得
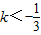 即为所求.
即为所求.点评:本题考查函数的恒成立问题,解题时要认真审题,仔细解答,注意合理地进行等价转化,同时注意函数性质的灵活运用.

练习册系列答案
相关题目
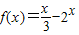 .
. .
.