题目内容
如图所示,线段
PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,△ACF的面积为72,求△BDE的面积.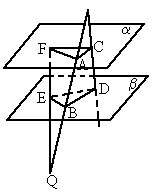
答案:84平方单位
解析:
解析:
|
求△ BCE的面积,看起来似乎与本节内容无关,事实上,已知△ACF的面积,若△BDE与△ACF的对应边有联系的话,可以利用△ACF的面积求出△BDE的面积.解:∵平面 QAF∩α=AF,平面QAF∩β=BE,又∵α∥β,∴ AF∥BE.同理可证 AC∥BD,∴∠FAC与∠EBD相等或互补,∴ sin∠FAC=sin∠EBD.由 FA∥BE,得BE∶AF=QB∶QA=12∶24=1∶2,∴ 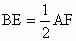 . .
由 BD∥AC,得AC∶BD=PA∶PB=9∶21=3∶7,∴ 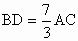 . .
又∵△ ACF的面积为72,即 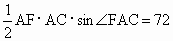 . .
∴△ BDE的面积为84平方单位.应用两个平面平行的性质,一是可以证明直线与直线的平行,二是可以解决线面平行的问题. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
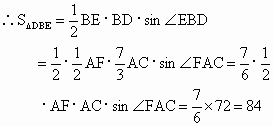
 ,P为线段CD上的一点(P与D不重合),过M、N、P的平面与直线BC交于Q,求证:BD∥PQ.
,P为线段CD上的一点(P与D不重合),过M、N、P的平面与直线BC交于Q,求证:BD∥PQ.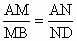 ,P为线段CD上的一点(P与D不重合),过M、N、P的平面与直线BC交于Q,求证:BD∥PQ.
,P为线段CD上的一点(P与D不重合),过M、N、P的平面与直线BC交于Q,求证:BD∥PQ.