题目内容
设f(x)的定义域是(-∞,0)∪(0,+∞),且f(x)对任意不为零的实数x都满足f(-x)=-f(x).已知当x>0时f(x)=
(1)求当x<0时,f(x)的解析式(2)解不等式f(x)<-
.
| x |
| 1-2x |
(1)求当x<0时,f(x)的解析式(2)解不等式f(x)<-
| x |
| 3 |
(1)当x<0时,-x>0,f(-x)=
=
又f(-x)=-f(x)
所以,当x<0时,f(x)=
(2)x>0时,f(x)=
<-
,∴
<-
化简得∴
<0,解得1<2x<4∴0<x<2
当x<0时,
<-
∴
>0解得2x>1(舍去)或2x<
∴x<-2
解集为{x|x<-2或0<x<2}
| -x |
| 1-2-x |
| -x2x |
| 2x-1 |
所以,当x<0时,f(x)=
| x•2x |
| 2x-1 |
(2)x>0时,f(x)=
| x |
| 1-2x |
| x |
| 3 |
| 1 |
| 1-2x |
| 1 |
| 3 |
化简得∴
| 4-2x |
| 3(1-2x) |
当x<0时,
| x2x |
| 2x-1 |
| x |
| 3 |
4(2x-
| ||
| 3(2x-1) |
| 1 |
| 4 |
∴x<-2
解集为{x|x<-2或0<x<2}

练习册系列答案
相关题目




 >1,则a_________1;若(
>1,则a_________1;若( )m<(0.125)n,则m_________n;若1.7a<1.7b,则a_________b.
)m<(0.125)n,则m_________n;若1.7a<1.7b,则a_________b. 及其反函数的图象与函数
及其反函数的图象与函数 的图象交于A、B两点,若
的图象交于A、B两点,若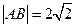 ,则实数a的值等于(精确到0.1 ,参考数据 lg2.414 ≈ 0.3827 lg 8.392 ≈ 0.9293 lg 8.41 ≈ 0.9247 )
,则实数a的值等于(精确到0.1 ,参考数据 lg2.414 ≈ 0.3827 lg 8.392 ≈ 0.9293 lg 8.41 ≈ 0.9247 ) 在
在 上的最大值与最小值之和为 .
上的最大值与最小值之和为 . .
. ,
, ,求
,求 的范围; (2)不等式
的范围; (2)不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 =____________
=____________