题目内容
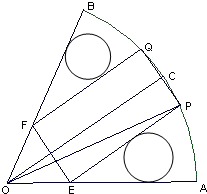 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为| π | 3 |
(1)试写出用θ表示长方形EPQF的面积S(θ)的函数;
(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形EPQF的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
分析:(1)在Rt△OPC中,OP=R,∠POC=θ,可求PC,OC,从而可得EF,EP,即可求长方形EPQF的面积,;
(2)制成圆柱的底面周长为EF,半径可求,△OEF的内切圆半径可求,两半径比较得出结论.
(2)制成圆柱的底面周长为EF,半径可求,△OEF的内切圆半径可求,两半径比较得出结论.
解答: 解:(1)由条件得CP=Rsinθ,EP=Rcosθ-
解:(1)由条件得CP=Rsinθ,EP=Rcosθ-
=Rcosθ-
Rsinθ,
从而S(θ)=2Rsinθ(Rcosθ-
Rsinθ).…(4分)
(2)由(1)得S(θ)=R2[sin2θ-
(1-cos2θ)]=2R2sin(2θ+
)-
R2,
所以当2θ+
=
时,即θ=
,S(θ)取得最大值,为(2-
)R2.…(7分)
此时EF=2Rsin
=
R,EP=Rcos
-
Rsin
=
R,
所以EPQF为正方形,依题意知制成的圆柱底面应是由EF围成的圆,
从而由周长2πr=EF=
R,得其半径为
R≈0.084R.…(11分)
另一方面,如图所示,设圆与OA边切于点H,连接GE、GH、GA,EA=OA-OE=
R.
设两小圆的半径为GH=r,则EH=
=(2+
)r,
且AH>r,从而(2+
)r+r<
R,所以r<
R≈0.10R,
因0.084R<0.10R,
所以能作出满足条件的两个圆.此时圆柱的体积V=
.…(16分)
 解:(1)由条件得CP=Rsinθ,EP=Rcosθ-
解:(1)由条件得CP=Rsinθ,EP=Rcosθ-| CP | ||
tan
|
| 3 |
从而S(θ)=2Rsinθ(Rcosθ-
| 3 |
(2)由(1)得S(θ)=R2[sin2θ-
| 3 |
| π |
| 3 |
| 3 |
所以当2θ+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 3 |
此时EF=2Rsin
| π |
| 12 |
| ||||
| 2 |
| π |
| 12 |
| 3 |
| π |
| 12 |
| ||||
| 2 |
所以EPQF为正方形,依题意知制成的圆柱底面应是由EF围成的圆,
从而由周长2πr=EF=
| ||||
| 2 |
| ||||
| 4π |
另一方面,如图所示,设圆与OA边切于点H,连接GE、GH、GA,EA=OA-OE=
2+
| ||||
| 2 |
设两小圆的半径为GH=r,则EH=
| r | ||
tan
|
| 3 |
且AH>r,从而(2+
| 3 |
2+
| ||||
| 2 |
2+
| ||||
2(3+
|
因0.084R<0.10R,
所以能作出满足条件的两个圆.此时圆柱的体积V=
(3
| ||||
| 8π |
点评:本题用柱体的侧面积和体积作为载体,重点考查了三角函数的运算与性质,求侧面积 S(θ)的最大值和柱体的体积时,考查了两角和与差的运算,且运算量较大,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个圆的面积之和,则
如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个圆的面积之和,则| lim |
| n→∞ |
| A、2πr2 | ||
B、
| ||
| C、4πr2 | ||
| D、6πr2 |
 如图,在半径为R的圆内随机撒一粒黄豆,它落在阴影部分内接正三角形上的概率是( )
如图,在半径为R的圆内随机撒一粒黄豆,它落在阴影部分内接正三角形上的概率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个正六边形的面积之和,则
如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个正六边形的面积之和,则 为前n个圆的面积之和,则
为前n个圆的面积之和,则

 B.
B.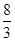
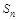 为前n
为前n 
 B.
B. C.
C. D.
D.