题目内容

．已知函数f(x)=lg[(a2－1)x2＋(a＋1)x＋1]，若f(x)的定义域为R，求实数a的取值范围．

 

【答案】

(－∞，－1]∪(，＋∞)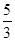

【解析】主要考查导数函数的概念、二次函数、对数函数的图象和性质。

解：依题意(a2－1)x2＋(a＋1)x＋1＞0对一切x∈R恒成立．

当a2－1≠0时，其充要条件是：

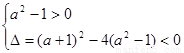解得a＜－1或a＞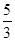

又a=－1，f(x)=0满足题意，a=1，不合题意．

所以a的取值范围是：(－∞，－1]∪(，＋∞)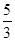

 

练习册系列答案
相关题目
已知函数f(x)=
3x+5，(x≤0)
x+5，(0＜x≤1)
-2x+8，(x＞1)
，
求（1）f(
1
π
)，f[f(-1)]的值；
（2）若f（a）＞2，则a的取值范围．
精英家教网已知函数f(x)=
(1-3a)x+10ax≤7
ax-7x＞7.
是定义域上的递减函数，则实数a的取值范围是（　　）
A、(
1
3
，1)
B、（
1
3
，
1
2
]
C、（
1
3
，
6
11
]
D、[
6
11
，1）
已知函数f(x)=
|x-1|-a
1-x2
是奇函数．则实数a的值为
 
．
已知函数f(x)=
2x-2-x2x+2-x

（1）求f（x）的定义域与值域；
（2）判断f（x）的奇偶性并证明；
（3）研究f（x）的单调性．
已知函数f(x)=
x-1x+a
+ln(x+1)，其中实数a≠1．
（1）若a=2，求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）若f（x）在x=1处取得极值，试讨论f（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网