题目内容
若不等式x2＋ax＋1³0对于一切xÎ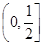
恒成立，则a的最小值是 （ ）
A．0 B．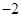
C．
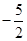D．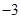
【答案】
C
【解析】
试题分析：将参数a与变量x分离，将不等式恒成立问题转化为求函数最值问题，即可得到结论。解：不等式x2+ax+1≥0对一切x∈(0，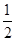
]成立，等价于a≥-x-
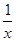对于一切x∈（0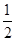，〕成立，∵y=-x-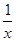在区间（0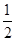，〕上是增函数，∴-x-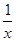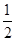＜--2=-
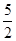∴a≥-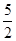∴a的最小值为-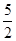故答案为C．
考点：不等式的应用
点评：本题综合考查了不等式的应用、不等式的解法等基础知识，考查运算求解能力，考查化归与转化思想，属于中档题
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
）成立，w.w.w.k.s.5.u.c.o.m 则a的取值范围是（ ）
D．-3
）成立，则a的取值范围是（ C ）
D.-3
）成立，则a的取值范围是 （ ）
D．-3
成立，则a的取值范围是
D．a≥－3
]成立，则a的取值范围是