题目内容
某商场一批进价30元/件的商品，在市场试销中发现，此商品的销售单价x元，与件数y（件）之间有如下关系：| x | … | 30 | 40 | 45 | 50 | … |
| y | … | 60 | 40 | 15 | 0 | … |
（II）设经营此商品的日销售利润为p（元），根据上述关系式写出p关于x的函数关系式，并求销售单价x为多少时，日销售利润最大？
分析：（I）由平面直角坐标系中画出的各点，猜测为一次函数，求出解析式后需要验证成立；
（II）销售利润函数=（售价-进价）×销量，代入数值得二次函数，求出最值．
（II）销售利润函数=（售价-进价）×销量，代入数值得二次函数，求出最值．
解答：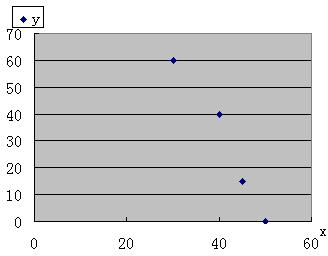
解：（I）在平面直角坐标系中画出各点，
如图，猜测为一次函数，
故设f（x）=kx+b（k，b为常数），
把点（30，60），（45，15）代入，
则
，解得：
∴f（x）=-3x+150．
（Ⅱ）日销售利润为：P=（x-30）•（-3x+150）=-3x2+240x-4500，30≤x≤50；
∵对称轴x=-
=40，
∴当销售单价为40元时，所获利润最大．
解：（I）在平面直角坐标系中画出各点，如图，猜测为一次函数，
故设f（x）=kx+b（k，b为常数），
把点（30，60），（45，15）代入，
则
|
|
∴f（x）=-3x+150．
（Ⅱ）日销售利润为：P=（x-30）•（-3x+150）=-3x2+240x-4500，30≤x≤50；
∵对称轴x=-
| 240 |
| -6 |
∴当销售单价为40元时，所获利润最大．
点评：本题考查了一次函数，二次函数的图象与性质，以及简单的作图能力，归纳猜想能力，是基础题．
练习册系列答案
相关题目
某商场经营一批进价是每件30元的商品，在市场销售中发现此商品的销售单
价x元与日销售量y件之间有如下关系：
（Ⅰ）在平面直角坐标系中，根据表中提供的数据描出实数对（x，y）对应的点，并确定x与y的一个函数关系式y=f（x）
（Ⅱ）设经营此商品的日销售利润为P元，根据上述关系式写出P关于x的函数关系式，并指出销售单价x为多少时，才能获得最大日销售利润．
价x元与日销售量y件之间有如下关系：
| 销售单价x（元） | 30 | 40 | 45 | 50 |
| 日销售量y（件） | 60 | 30 | 15 | 0 |
（Ⅱ）设经营此商品的日销售利润为P元，根据上述关系式写出P关于x的函数关系式，并指出销售单价x为多少时，才能获得最大日销售利润．
某商场一批进价30元/件的商品，在市场试销中发现，此商品的销售单价x元，与件数y（件）之间有如下关系：
| x | … | 30 | 40 | 45 | 50 | … |
| y | … | 60 | 40 | 15 | 0 | … |
（II）设经营此商品的日销售利润为p（元），根据上述关系式写出p关于x的函数关系式，并求销售单价x为多少时，日销售利润最大？
某商场一批进价30元/件的商品，在市场试销中发现，此商品的销售单价x元，与件数y（件）之间有如下关系：
（I）在所给的平面直角坐标系中，根据表中的数据做出实数对（x，y）对应的点，猜想它们之间的函数关系，并确定y与x的一个函数关系；
（II）设经营此商品的日销售利润为p（元），根据上述关系式写出p关于x的函数关系式，并求销售单价x为多少时，日销售利润最大？
| x | … | 30 | 40 | 45 | 50 | … |
| y | … | 60 | 40 | 15 | … |
（II）设经营此商品的日销售利润为p（元），根据上述关系式写出p关于x的函数关系式，并求销售单价x为多少时，日销售利润最大？