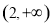题目内容
2．已知集合A={x|x2-2x-3≥0}，B={x|-4≤x≤2}，则集体B∩∁RA=（ ）| A． | （-1，2] | B． | ∅ | C． | [-4，-1] | D． | [-4，3） |
分析 求出A中不等式的解集确定出A，进而求出A的补集，找出B与A补集的交集即可．
解答 解：由A中不等式变形得：（x-3）（x+1）≥0，
解得：x≤-1或x≥3，即A=（-∞，-1]∪[3，+∞），
∴∁RA=（-1，3），
∵B=[-4，2]，
∴B∩∁RA=（-1，2]，
故选：A．
点评 此题考查了交、并、补集的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
15．已知f（x）是定义在R上的奇函数，若x1，x2∈R，则“x1+x2=0”是“f（x1）+f（x2）=0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
10．在复平面内，复数z=1-2i对应的点的坐标为（ ）
| A． | （1，2） | B． | （2，1） | C． | （1，-2） | D． | （2，-1） |
17．双曲线x2-my2=1的实轴长是虚轴长的2倍，则m=（ ）
| A． | 4 | B． | 2 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
7．已知i是虚数单位，复数$\frac{1+i}{2-i}$=（ ）
| A． | $\frac{1}{5}-\frac{3}{5}$i | B． | $\frac{3}{5}+\frac{1}{5}$i | C． | $\frac{1}{3}+\frac{2}{3}$i | D． | $\frac{1}{5}+\frac{3}{5}$i |
的单调递减区间是（ ）
B．
D．