题目内容
设f(x)=xlogax+(1-x)loga(1-x)(a>1)
(1)判断f(x)的单调性;
(2)已知m+n=4,且m>0,n>0,求mlog4m+nlog4n的最小值.
解:(1)由f′(x)=logax+ -loga(1-x)-
-loga(1-x)- =logax-loga(1-x)=loga
=logax-loga(1-x)=loga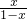
令f′(x)=0得x=
∵a>1,∴当0<x< 时,
时,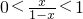 ,f′(x)<0;同理,当
,f′(x)<0;同理,当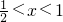 时,f′(x)>0
时,f′(x)>0
∴f(x)在(0, )上递减,在(
)上递减,在( ,1)上递增…(6分)
,1)上递增…(6分)
(2)由(1)知,f(x)在x= 处取最小值,f(x)min=f(
处取最小值,f(x)min=f( )=loga
)=loga
令m=4m1,n=4n1,则m1+n1=1,所以mlog4m+nlog4n=4[1+m1log4m1+(1-m1)log4(1-m1)]≥4(1+log4 )=2
)=2
∴mlog4m+nlog4n的最小值为2.…(12分)
分析:(1)求导函数,令f′(x)=loga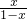 =0得x=
=0得x= ,利用导数的正负,即可确定函数的单调性;
,利用导数的正负,即可确定函数的单调性;
(2)由(1)知,f(x)在x= 处取最小值,f(x)min=f(
处取最小值,f(x)min=f( )=loga
)=loga ,令m=4m1,n=4n1,则m1+n1=1,所以mlog4m+nlog4n=4[1+m1log4m1+(1-m1)log4(1-m1)],由此可得结论.
,令m=4m1,n=4n1,则m1+n1=1,所以mlog4m+nlog4n=4[1+m1log4m1+(1-m1)log4(1-m1)],由此可得结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查最值的求解,解题的关键是求导确定函数的最值.
 -loga(1-x)-
-loga(1-x)- =logax-loga(1-x)=loga
=logax-loga(1-x)=loga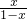
令f′(x)=0得x=

∵a>1,∴当0<x<
 时,
时,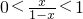 ,f′(x)<0;同理,当
,f′(x)<0;同理,当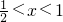 时,f′(x)>0
时,f′(x)>0∴f(x)在(0,
 )上递减,在(
)上递减,在( ,1)上递增…(6分)
,1)上递增…(6分)(2)由(1)知,f(x)在x=
 处取最小值,f(x)min=f(
处取最小值,f(x)min=f( )=loga
)=loga
令m=4m1,n=4n1,则m1+n1=1,所以mlog4m+nlog4n=4[1+m1log4m1+(1-m1)log4(1-m1)]≥4(1+log4
 )=2
)=2∴mlog4m+nlog4n的最小值为2.…(12分)
分析:(1)求导函数,令f′(x)=loga
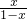 =0得x=
=0得x= ,利用导数的正负,即可确定函数的单调性;
,利用导数的正负,即可确定函数的单调性;(2)由(1)知,f(x)在x=
 处取最小值,f(x)min=f(
处取最小值,f(x)min=f( )=loga
)=loga ,令m=4m1,n=4n1,则m1+n1=1,所以mlog4m+nlog4n=4[1+m1log4m1+(1-m1)log4(1-m1)],由此可得结论.
,令m=4m1,n=4n1,则m1+n1=1,所以mlog4m+nlog4n=4[1+m1log4m1+(1-m1)log4(1-m1)],由此可得结论.点评:本题考查导数知识的运用,考查函数的单调性,考查最值的求解,解题的关键是求导确定函数的最值.

练习册系列答案
相关题目