题目内容
半径不等的两定圆 、
、 无公共点(
无公共点( 、
、 是两个不同的点),动圆
是两个不同的点),动圆 与圆
与圆 、
、 都内切,则圆心
都内切,则圆心 轨迹是( )
轨迹是( )
A.双曲线的一支 B.椭圆或圆
C.双曲线的一支或椭圆或圆 D.双曲线一支或椭圆
【答案】
D
【解析】
试题分析:设定圆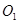 、
、 的半径分别为
的半径分别为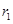 、
、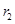 ,不妨设
,不妨设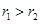 ,由于两定圆
,由于两定圆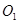 、
、 无公共点,则圆
无公共点,则圆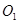 、
、 相离或内含,设动圆
相离或内含,设动圆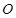 的半径为
的半径为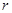 ,则
,则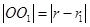 ,
,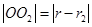 ,
,
若定圆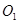 、
、 相离,则
相离,则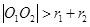 ,则定圆
,则定圆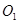 、
、 同时内切于动圆
同时内切于动圆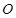 ,则
,则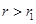 ,
,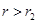 ,则
,则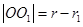 ,
,
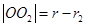 ,则
,则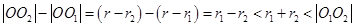 ,此时动点
,此时动点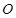 的轨迹是双曲线的一支;
的轨迹是双曲线的一支;
若定圆 内含于圆
内含于圆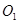 ,则
,则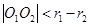 ,此时动圆
,此时动圆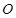 内切于定圆
内切于定圆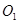 ,定圆
,定圆 内切于动圆
内切于动圆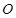 ,则
,则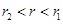 ,
,
则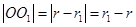 ,
,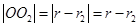 ,
,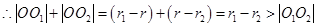 ,此时动点
,此时动点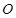 的轨迹是椭圆,故选D.
的轨迹是椭圆,故选D.
考点:1.两圆内切;2.椭圆与双曲线的定义

练习册系列答案
相关题目
半径不等的两定圆O1、O2无公共点(O1、O2是两个不同的点),动圆O与圆O1、O2都内切,则圆心O轨迹是( )
| A、双曲线的一支 | B、椭圆或圆 | C、双曲线的一支或椭圆或圆 | D、双曲线一支或椭圆 |