题目内容
已知函数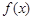 的导函数是
的导函数是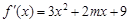 ,
,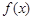 在
在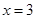 处取得极值,且
处取得极值,且
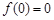 ,
,
(Ⅰ)求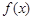 的极大值和极小值;
的极大值和极小值;
(Ⅱ)记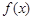 在闭区间
在闭区间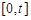 上的最大值为
上的最大值为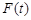 ,若对任意的
,若对任意的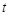
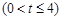 总有
总有
 成立,求
成立,求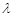 的取值范围;
的取值范围;
(Ⅲ)设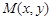 是曲线
是曲线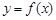 上的任意一点.当
上的任意一点.当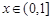 时,求直线OM斜率的最
时,求直线OM斜率的最
小值,据此判断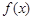 与
与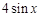 的大小关系,并说明理由.
的大小关系,并说明理由.
【答案】
(Ⅰ)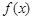 的极大值和极小值分别为4和0 (Ⅱ)
的极大值和极小值分别为4和0 (Ⅱ)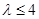
(Ⅲ)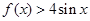
【解析】
试题分析:(I)依题意,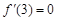 ,解得
,解得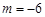 ,
,
由已知可设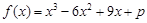 ,因为
,因为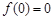 ,所以
,所以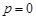 ,
,
则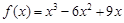 ,导函数
,导函数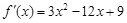 .
.
列表:
|
|
|
1 |
(1,3) |
3 |
(3,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
|
递增 |
极大值4 |
递减 |
极小值0 |
递增 |
由上表可知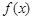 在
在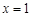 处取得极大值为
处取得极大值为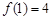 ,
,
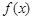 在
在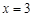 处取得极小值为
处取得极小值为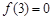 .
.
(Ⅱ)①当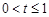 时,由(I)知
时,由(I)知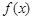 在
在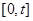 上递增,
上递增,
所以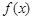 的最大值
的最大值 ,
,
由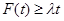 对任意的
对任意的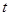 恒成立,得
恒成立,得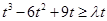 ,则
,则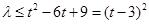 ,
,
因为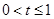 ,所以
,所以 ,则
,则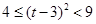 ,
,
因此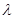 的取值范围是
的取值范围是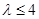 .
.
②当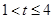 时,因为
时,因为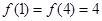 ,所以
,所以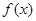 的最大值
的最大值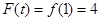 ,
,
由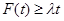 对任意的
对任意的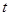 恒成立,得
恒成立,得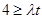 ,∴
,∴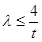 ,
,
因为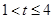 ,所以
,所以 ,因此
,因此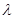 的取值范围是
的取值范围是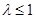 ,
,
综上①②可知,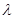 的取值范围是
的取值范围是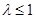 .
.
(Ⅲ)当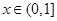 时,直线
时,直线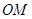 斜率
斜率 ,
,
因为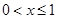 ,所以
,所以 ,则
,则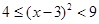 ,
,
即直线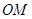 斜率的最小值为4
斜率的最小值为4
首先,由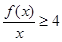 ,得
,得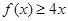 .
.
其次,当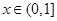 时,有
时,有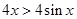 ,所以
,所以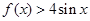 ,
,
证明如下:记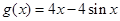 ,则
,则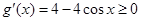 ,
,
所以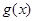 在
在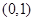 递增,又
递增,又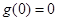 ,
,
则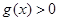 在
在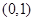 恒成立,即
恒成立,即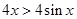 ,所以
,所以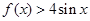 .
.
考点:利用导数求闭区间上函数的最值;利用导数研究函数的极值.
点评:本题考查导数的应用,考查函数极值的求法,考查实数的取值范围的求法,考查两个数比较大小的方法.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
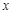
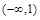
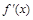
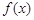 的导函数是
的导函数是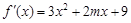 ,
, 处取得极值,且
处取得极值,且 .
. 上的最大值为
上的最大值为 ,若对任意的
,若对任意的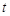
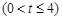 总有
总有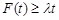 成立,求
成立,求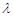 的取值范围;
的取值范围; 是曲线
是曲线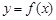 上的任意一点.当
上的任意一点.当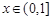 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 的大小关系,并说明理由.
的大小关系,并说明理由.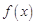 的导函数
的导函数 是二次函数,当
是二次函数,当 时,
时,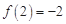 .
.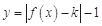 有两个零点,求实数
有两个零点,求实数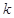 的取值范围;
的取值范围;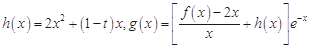 ,若存在实数
,若存在实数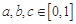 ,使得
,使得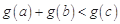 ,求
,求 的取值范围.
的取值范围. 的导函数是
的导函数是 ,设
,设 是方程
是方程 的两根.若
的两根.若 ,
,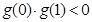 ,则|
,则| |的取值范围为
.
|的取值范围为
.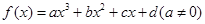 的导函数是
的导函数是 ,
, . 设
. 设 是方程
是方程 的两根,则|
的两根,则|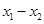 |的取值范围为 .
|的取值范围为 .