题目内容
已知函数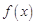 的导函数
的导函数 是二次函数,当
是二次函数,当 时,
时,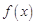 有极值,且极大值为2,
有极值,且极大值为2,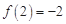 .
.
(1)求函数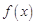 的解析式;
的解析式;
(2)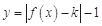 有两个零点,求实数
有两个零点,求实数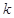 的取值范围;
的取值范围;
(3)设函数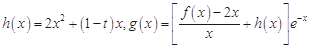 ,若存在实数
,若存在实数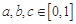 ,使得
,使得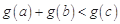 ,求
,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)先通过函数 的导函数
的导函数 是二次函数,且当
是二次函数,且当 时,
时, 有极值将函数
有极值将函数 的导函数设出来:
的导函数设出来: .从而可设
.从而可设 ,其中
,其中 为常数.再由
为常数.再由 极大值为2及
极大值为2及 将
将 求出.注意,
求出.注意, 极大值为2,即
极大值为2,即 或
或 时,函数值为2.结合
时,函数值为2.结合 正好可以将其中一种情况舍去,从而解出
正好可以将其中一种情况舍去,从而解出 ,于是得到函数
,于是得到函数 的解析式;(2)由
的解析式;(2)由 ,
, 列出表格,分析函数
列出表格,分析函数 的单调性和极值.
的单调性和极值. 有两个零点,即方程
有两个零点,即方程 有两个根,而
有两个根,而 ,即方程
,即方程 与方程
与方程 各只有一个解.结合函数
各只有一个解.结合函数 的单调性和极值,发现方程
的单调性和极值,发现方程 只有当
只有当 或
或 时才只有一个解.所以有
时才只有一个解.所以有 或
或 或
或 ,从而解得
,从而解得 或
或 ;(3)由于存在实数
;(3)由于存在实数 ,使得
,使得 ,也就是说
,也就是说 ,否则就不存在实数
,否则就不存在实数 ,使得
,使得 .因此本题转化为求
.因此本题转化为求 在
在 上的最大值与最小值.根据条件可得
上的最大值与最小值.根据条件可得 ,所以其导函数
,所以其导函数 .然后讨论
.然后讨论 的范围以得到
的范围以得到 在
在 上单调性,从而找出最值.再通过不等式
上单调性,从而找出最值.再通过不等式 得到
得到 的取值范围.注意当
的取值范围.注意当 时比较麻烦,
时比较麻烦, 在
在 上先减后增,
上先减后增,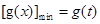 ,而最大值无法确定是
,而最大值无法确定是 中的哪一个,所以我们用
中的哪一个,所以我们用 来表示不等式
来表示不等式 .
.
试题解析:(1)由条件,可设 ,则
,则 ,其中
,其中 为常数.
为常数.
因为 极大值为2.所以
极大值为2.所以 或
或 ,即
,即 或
或 .由
.由 得
得 ①.所以
①.所以 ,即
,即 ②.由①②可得,
②.由①②可得, .所以
.所以 .
.
(2)由(1),得 ,即
,即 .列表:
.列表:
|
|
|
-1 |
(-1,0) |
1 |
|
|
|
- |
0 |
+ |
0 |
- |
|
|
|
极小值-2 |
|
极大值2 |
|
又因为函数 有两个根,即方程
有两个根,即方程 有两个根,而
有两个根,而 ,
,
所以 或
或 或
或 ,解得
,解得 或
或 .
.
所以若函数 有两个零点,实数
有两个零点,实数 的取值范围为
的取值范围为 .
.
(3)由于存在实数 ,使得
,使得 ,则问题等价于
,则问题等价于 .
.
 ,
,
 ,
, .在
.在 上,
上,
当 时,
时, ,
, 在
在 上递减,
上递减,
 ,即
,即 ,得
,得 .
.
当 时,
时, ,
, 在
在 上递增,
上递增,
 ,即
,即 ,得
,得 .
.
当 时,在
时,在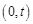 上
上 ,
, 递减;在
递减;在 上
上 ,
, 递增.
递增.
 ,即
,即 .(*)
.(*)
 ,
, 在
在 上递减,
上递减, .
.
 ,而
,而 ,不等式(*)无解.
,不等式(*)无解.
综上所述,存在 ,使得命题成立.
,使得命题成立.
考点:1.函数的极值、最值;2.利用导数研究函数的单调性;3.常见函数的导数及导数的运算法则.







 (2012•青岛二模)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图示.
(2012•青岛二模)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图示.