题目内容
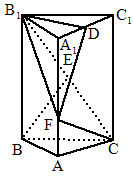
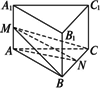
如下图所示,直三棱柱ABC-A1B1C1中,底面为等腰三角形,底边BC长为a,过BC作与底面成![]() 角(0<
角(0<![]() <
<![]() )的平面交AA1于M,若截得的锥体M-ABC的体积为V,求截面△MBC的面积.
)的平面交AA1于M,若截得的锥体M-ABC的体积为V,求截面△MBC的面积.
答案:
解析:
提示:
解析:
|
解:∵MA⊥平面ABC,且AB=AC,∴MB=MC 设BC的中点为N,连结AN、MN,则AN⊥BC,MN⊥BC,故∠ANM= 思路分析:在本题中,可用MN表示三棱锥M-ABC的高AM,故可利用体积求MN. |
提示:
|
在解决有关柱、锥、台体问题时,可把某些平面图形分离出来,运用平面几何的相关知识去解决,这是解决立体几何中计算问题的重要方法和技巧. |

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目

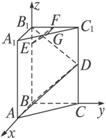
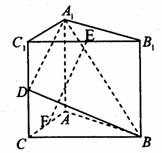
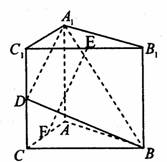
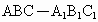 中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,
中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,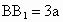 ,D为
,D为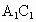 的中点,E为
的中点,E为 的中点.
的中点.
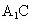 所成的角的余弦值;
所成的角的余弦值;
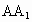 上是否存在点F,使CF⊥平面
上是否存在点F,使CF⊥平面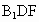 ,若存在,求出AF的长;若不存在,说明理由.
,若存在,求出AF的长;若不存在,说明理由.