题目内容
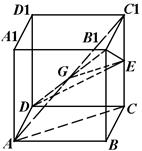
在棱长为2的正方体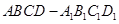 中,设
中,设 是棱
是棱 的中点.
的中点.
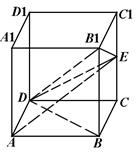
⑴ 求证: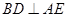 ;
;
⑵ 求证: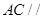 平面
平面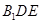 ;
;
⑶ 求三棱锥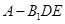 的体积.
的体积.
【答案】
⑴连接BD,AE. 故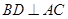 ,因
,因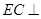 底面ABCD,故
底面ABCD,故 ,故
,故 平面
平面 故
故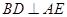 ⑵连接
⑵连接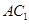 ,设
,设 ,连接
,连接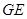 ,则
,则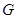 为
为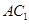 中点,而
中点,而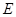 为
为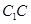 的中点,则
的中点,则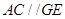 故
故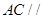 平面
平面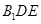 ⑶
⑶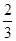
【解析】
试题分析:(1)连接BD,AE. 因四边形ABCD为正方形,故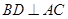 ,
, 
因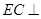 底面ABCD,
底面ABCD,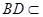 面ABCD,故
面ABCD,故 ,又
,又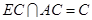 ,
,
故 平面
平面 ,
,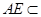 平面
平面 ,故
,故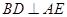 .
.
⑵. 连接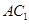 ,设
,设 ,连接
,连接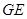 ,
,
则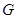 为
为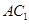 中点,而
中点,而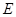 为
为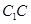 的中点,故
的中点,故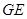 为三角形
为三角形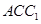 的中位线,
的中位线,
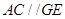 ,
,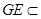 平面
平面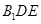 ,
,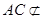 平面
平面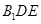 ,故
,故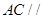 平面
平面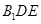 .
.
⑶. 由⑵知,点A到平面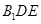 的距离等于C到平面
的距离等于C到平面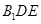 的距离,故三棱锥
的距离,故三棱锥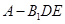 的体积
的体积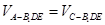 ,而
,而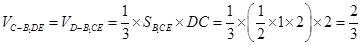 ,三棱锥
,三棱锥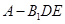 的体积为
的体积为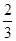 .
.
考点:线面平行垂直的判定与性质及锥体的体积
点评:要证明线面平行常借助于平面外一直线与平面内一直线平行;线面的垂直关系中常用的思路是线线垂直与线面垂直的互相转化;第三问求三棱锥体积时采用等体积法的思路转化底面和顶点,是底面积和高都容易求出

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
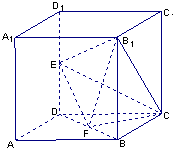 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.  到平面
到平面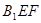 的距离等于( )
的距离等于( )
 B.
B. C.
C. D.
D.
 中,点
中,点 为底面
为底面 的中心,在正方体
的中心,在正方体 ,则点
,则点 中,动点
中,动点 在
在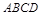 内,且到直线
内,且到直线 的距离之和等于
的距离之和等于 ,则
,则 的面积最大值是 ( )
的面积最大值是 ( ) B.1 C.2 D.4
B.1 C.2 D.4 中,
中, 为底面的中心,
为底面的中心, 是
是 的中点,那么异面直线
的中点,那么异面直线 与
与 所成角的余弦值为
所成角的余弦值为
 (B)
(B)  (C)
(C)  (D)
(D)
