题目内容

若角α、β满足-
π
2
＜α＜β＜π，则α-β的取值范围是
(-
3π
2
，0)
(-
3π
2
，0)
．
分析：角α、β满足-
π
2
＜α＜β＜π，求出-β的范围，可得α-β＜0，从而进行求解；
解答：解：∵角α、β满足-
π
2
＜α＜β＜π，
∴-π＜-β＜-
π
2
，
∴-
3
2
π＜α-β＜
π
2
，∵α-β＜0，
∴-
3
2
＜α-β＜0，
故答案为：(-
3π
2
，0)；
点评：此题主要考查函数的值域求法，注意α-β是小于0的，此题是一道基础题；
练习册系列答案
相关题目
已知函数f（x）=sinx，x∈R．
（1）求函数f（x）的最小正周期和最大值；
（2）若θ为第一象限的角，且满足f(θ)=
3
5
，求f(θ-
π
4
)的值．
若角θ、Φ满足-
π
2
＜θ＜Φ＜
π
2
，则2θ-Φ的取值范围是
m
（-
3π
2
，
π
2
）
（-
3π
2
，
π
2
）
．
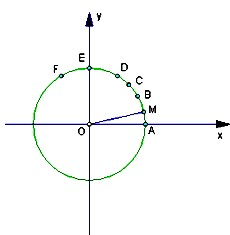如图，圆O为单位圆，A（1，0），B(
3
2
，
1
2
)，C(
2
2
，
2
2
)，D(
1
2
，
3
2
)，E（0，1），F(-
1
2
，
3
2
)为圆O上的定点，点M为圆O上的动点．M第一次由点A按逆时针方向运动到某定点，所形成的角为α；M第二次由点A按逆时针方向运动到某定点，所形成的角为β．
（Ⅰ） 当点M第一次由点A按逆时针方向运动到定点C，第二次由点A按逆时针方向运动到定点D时，求cos（α-β）的值；
（Ⅱ）在A、B、C、D、E、F中是否存在两个点，能使角α，β同时满足α+2β=
3π
2
，且tan
α
2
tanβ=3-2
3
．若不存在，说明理由； 若存在，找出定点并证明．
已知
m
=(1，sin2x)，
n
=(cos2x，
3
)，f(x)=
m
•
n
．锐角△ABC的三内角A、B、C对应的三边分别为a、b、c．满足：f（A）=1．
（1）求角A；
（2）若a=2，△ABC的面积为
3
，求边b、c的值．
有下列命题：
①G=
ab
（G≠0）是a，G，b成等比数列的充分非必要条件；
②若角α，β满足cosαcosβ=1，则sin（α+β）=0；
③若不等式|x-4|+|x-3|＜a的解集非空，则必有a≥1；
④函数y=sinx+sin|x|的值域是[-2，2]．
其中正确命题的序号是
①②③④
①②③④
．（把你认为正确的命题的序号都填上）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网